Геометрические расчеты конических зубчатых колес
Геометрические расчеты конических колес аналогичны расчетам цилиндрических. Число зубьев плоского колеса 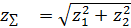 (может получиться дробным). Вместо начальных и делительных цилиндров цилиндрических колес в конических колесах вводятся понятия начальный и делительный конусы, которые, как правило, совпадают, так как для конических колес угловую коррекцию практически не применяют. В качестве торцовых сечений рассматривают сечения поверхностями дополнительных конусов, т. е. конусов, оси которых совпадают с осью колеса, а образующие перпендикулярны к образующим делительного конуса (рисунок 3.16). Также используются понятия внешнего и внутреннего дополнительных конусов (ограничивающих зубчатый венец) и среднего дополнительного конуса. Действительные профили зубьев конических колес весьма близки к профилям воображаемых эквивалентных цилиндрических колес с радиусами делительных окружностей, равными длинам образующих дополнительных конусов.
(может получиться дробным). Вместо начальных и делительных цилиндров цилиндрических колес в конических колесах вводятся понятия начальный и делительный конусы, которые, как правило, совпадают, так как для конических колес угловую коррекцию практически не применяют. В качестве торцовых сечений рассматривают сечения поверхностями дополнительных конусов, т. е. конусов, оси которых совпадают с осью колеса, а образующие перпендикулярны к образующим делительного конуса (рисунок 3.16). Также используются понятия внешнего и внутреннего дополнительных конусов (ограничивающих зубчатый венец) и среднего дополнительного конуса. Действительные профили зубьев конических колес весьма близки к профилям воображаемых эквивалентных цилиндрических колес с радиусами делительных окружностей, равными длинам образующих дополнительных конусов.
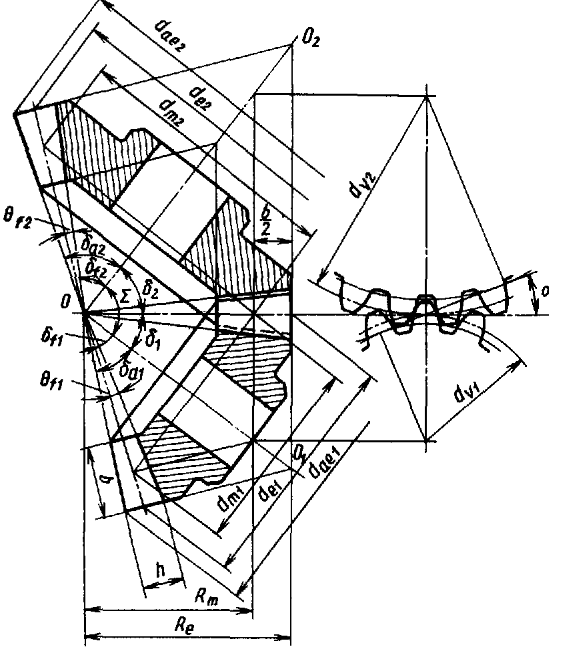
 – внешнее конусное расстояние; b – ширина зубчатого вернца;
– внешнее конусное расстояние; b – ширина зубчатого вернца;  – среднее конусное расстояние;
– среднее конусное расстояние; 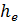 – наибольшая высота зубьев (у торца);
– наибольшая высота зубьев (у торца); 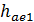 – наибольшая высота головки;
– наибольшая высота головки; 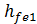 – наибольшая высота ножки зубьев (у торца);
– наибольшая высота ножки зубьев (у торца); 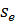 – окружная толщина зуба по внешней делительной окружности;
– окружная толщина зуба по внешней делительной окружности; 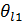 - угол ножки зубьев;
- угол ножки зубьев; 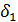 – угол делительного (начального) конуса;
– угол делительного (начального) конуса; 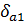 – угол конуса вершин;
– угол конуса вершин; 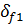 – угол конуса впадин;
– угол конуса впадин; 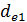 - диаметр внешней делительной окружности;
- диаметр внешней делительной окружности; 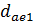 - диаметр внешних вершин
- диаметр внешних вершин
Рисунок 3.17 – Схема к геометрическому расчету конических передач
Зубья конических колес по признаку изменения размеров сечений по длине выполняют трех форм (рисунок 3.18):
- Осевая форма I ‒ нормально понижающиеся зубья; вершины делительного и внутреннего конусов совпадают (рисунок 3.18, а). Эту форму применяют для конических передач с прямыми и тангенциальными зубьями, а также ограничено для передач с круговыми зубьями при 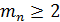 и
и 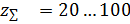 .
.
- Осевая форма II ‒ вершина внутреннего конуса располагается так, что ширина дна впадины колеса постоянна, а толщина зуба по делительному конусу растет с увеличением расстояния от вершины. Эта форма позволяет обрабатывать одним инструментом сразу обе поверхности зубьев колеса. Поэтому она является основной для колес с круговыми зубьями, широко применяется в массовом производстве.
- Осевая форма III (рисунок 3.18, в) ‒ равновысокие зубья; образующие делительного и внутреннего конусов параллельны. Эту форму применяют для круговых зубьев при 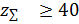 , в частности при средних конусных расстояниях 75-750 мм.
, в частности при средних конусных расстояниях 75-750 мм.
Формы II и III получают смещением вершины конуса впадин и вершины делительного конуса (рисунок 3.18 б, в).
Рисунок 3.18 – Формы зубьев конических передач
У конических колес удобно измерять, а потому и задавать размеры зубьев на внешнем дополнительном конусе. В зубчатых колесах с зубьями формы I обычно оперируют окружным модулем 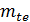 на виешнем торце. В зубчатых колесах с зубьями формы II и III преимущественно оперируют нормальным модулем
на виешнем торце. В зубчатых колесах с зубьями формы II и III преимущественно оперируют нормальным модулем 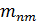 , на середине ширины зубчатого венца. Круговые зубья нарезают немодульным инструментом, позволяющим обрабатывать зубья в некотором диапазоне модулей. Поэтому допускается применять передачи с нестандартными и дробными модулями. Соотношение между модулями
, на середине ширины зубчатого венца. Круговые зубья нарезают немодульным инструментом, позволяющим обрабатывать зубья в некотором диапазоне модулей. Поэтому допускается применять передачи с нестандартными и дробными модулями. Соотношение между модулями 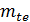 и
и 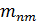 , следующее:
, следующее:
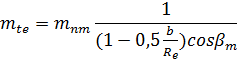
где Р - внешнее конусное расстояние .Угол наклона линии зуба выбирают, учитывая, что увеличение улучшает плавность зацепления, но при этом возрастают усилия. При круговых зубьях преимущественно применяют 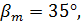 а при тангенциальных 20...30°, обычно угол
а при тангенциальных 20...30°, обычно угол 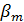 выбирают кратным 5°. Минимально допустимые числа зубьев приведены в таблице 3.1. Для уменьшения шума рекомендуют применять притирку и выбирать некратные числа зубьев колес. Для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни
выбирают кратным 5°. Минимально допустимые числа зубьев приведены в таблице 3.1. Для уменьшения шума рекомендуют применять притирку и выбирать некратные числа зубьев колес. Для зубчатых передач с твердостью рабочих поверхностей зубьев шестерни 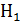 , и колеса
, и колеса 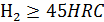 число зубьев шестерни рекомендуют выбирать в зависимости от внешнего делительного диаметра шестерни
число зубьев шестерни рекомендуют выбирать в зависимости от внешнего делительного диаметра шестерни 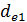 , при твердости
, при твердости 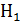 и
и 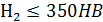 выбранные значения
выбранные значения 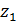 увеличивают в 1,6 раза; при
увеличивают в 1,6 раза; при 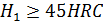 и
и 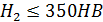
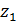 увеличивают в 1,3 раза. Основные геометрические соотношения в конических передачах приведены в таблицах 3.1-3.3. Корригирование конических зацеплений по сравнению с цилиндрическими имеет следующие особенности. Область целесообразного применения высотной коррекции конических зацеплений расширена. Наоборот, угловая коррекция, при которой сумма смещений исходного контура для колес не равна нулю, весьма трудно осуществима из-за необходимости сохранить заданный межосевой угол, поэтому ее практически не применяют. Для конических зацеплений, в отличие от цилиндрических, при u > 2,5 удобно применять так называемую тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответственном толщине зуба колеса. Тангенциальная коррекция конических колес не требует специального инструмента, так как ее получают благодаря разведению резцов, обрабатывающих противоположные стороны зубьев. Для цилиндрических колес тангенциальную коррекцию не применяют, так как она требует специального инструмента.
увеличивают в 1,3 раза. Основные геометрические соотношения в конических передачах приведены в таблицах 3.1-3.3. Корригирование конических зацеплений по сравнению с цилиндрическими имеет следующие особенности. Область целесообразного применения высотной коррекции конических зацеплений расширена. Наоборот, угловая коррекция, при которой сумма смещений исходного контура для колес не равна нулю, весьма трудно осуществима из-за необходимости сохранить заданный межосевой угол, поэтому ее практически не применяют. Для конических зацеплений, в отличие от цилиндрических, при u > 2,5 удобно применять так называемую тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответственном толщине зуба колеса. Тангенциальная коррекция конических колес не требует специального инструмента, так как ее получают благодаря разведению резцов, обрабатывающих противоположные стороны зубьев. Для цилиндрических колес тангенциальную коррекцию не применяют, так как она требует специального инструмента.
| Таблица 3.1 - Основные размеры конических зубчатых колес с прямыми, тангенциальными и круговыми понижающимися зубьями (осевая форма зубьев 1) при межосевом угле ∑=90° | |||
| Параметр зацепления | Формула | ||
| Внешнее конусное расстояние | 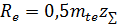
| ||
| Ширина венца | 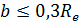
| ||
| Среднее конусное расстояние | 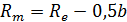
| ||
| Наибольшая высота: зубьев (у торца) |
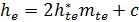 , где , где 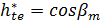 ; c=0,2 ; c=0,2 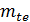
| ||
| головки зубьев (у торца) | 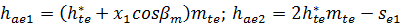
| ||
| ножки зубьев (у торца) | 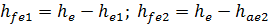
| ||
| Окружная толщина зуба по внешней делительной окружности | 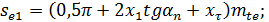
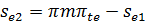
| ||
| Угол: ножки зубьев | 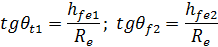
| ||
| делительного (начального) конуса | 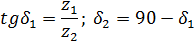
| ||
| конуса вершин | 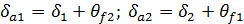
| ||
| конуса впадин | 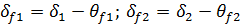
| ||
Окончание таблицы 3.1
| Диаметр: внешней делительной окружности | 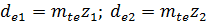
|
| внешний вершин | 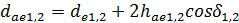
|
| Расчетное базовое расстояние (от вершины делительного конуса до основания наружного конуса) |
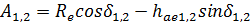
|
| Эксцентриситет для тангенциальных зубьев | 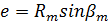
|
| Угол наклона: тангенциальных зубьев у торца | 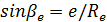
|
| круговых зубьев | 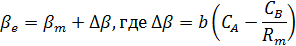
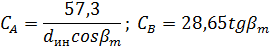
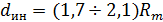
|
| Таблица 3.2 ‒ Основные размеры конических зубчатых колес с постоянной шириной дна впадины (осевая форма зубьев II) | |
| Параметр зацепления | Формула |
| Среднее конусное расстояние | 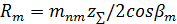
|
| Ширина зубчатого венца | 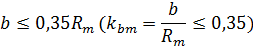
|
| Внешняя конусная дистанция | 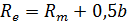
|
| Высота головки зуба посередине ширины венца | 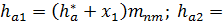
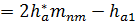
|
| Окружная толщина зуба а среднем нормальном сечении | 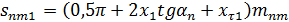
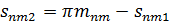
|
Окончание таблицы 3.2
Промежуточная расчетная величина (определяется при 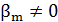 и округляется до целого числа, кратного 10) и округляется до целого числа, кратного 10)
| 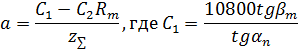
|
| Сумма углов ножек зубьев шестерни и колеса в минутах | при 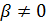 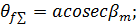 при
при 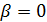 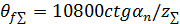
|
| Угол ножки зуба (округлить до 1) | 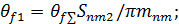 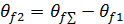
|
| Поправка высоты головки при переходе на внешний конус | 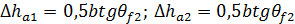
|
| Наибольшая высота: головки зубьев (по торцу) | 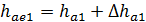 ; ; 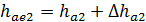
|
| зуба по торцу | 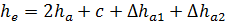 ; ;
|
| Таблица 3.3 ‒ Основные размеры конических зубчатых колес с равновысокими зубьями (осевая форма зубьев III) | ||
| Параметр зацепления | Формула | |
| Высота зуба | 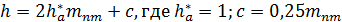
| |
| Высота головки зуба | 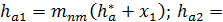
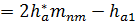
| |
| Угол начального наружного и внутреннего конусов | 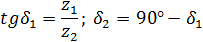
| |
| Окружная толщина зуба в среднем нормальном сечении | 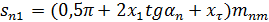
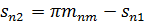
| |
Примечание. Величины 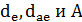 определяют так же, как при осевой форме зуба I определяют так же, как при осевой форме зуба I
|
Практически для конических зубчатых зацеплений применяют высотную коррекцию в сочетании с тангенциальной. Для повышения износостойкости и сопротивления зубьев заеданию с помощью высотной коррекции выравнивают удельные скольжения зубьев шестерни и колеса, а с помощью тангенциальной коррекции выравнивают прочность зубьев шестерни колеса. На этом основана система коррекции ЭНиМС конических передач с прямыми, тангенциальными и круговыми зубьями. Рекомендуемый коэффициент радиального смещения у шестерни:
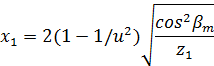
Коэффициент тангенциального смещения у шестерни при 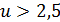 :
:
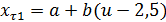
где при 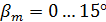
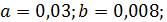
при 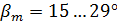 соответственно 0,07 и 0,010;
соответственно 0,07 и 0,010;
при 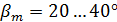 соответственно 0,11 и 0,010
соответственно 0,11 и 0,010
Дата добавления: 2015-02-05; просмотров: 13001;
