Расчет зубьев на контактную прочность. Расчет сводится к удовлетворению условия, по которому контактные напряжения зубьев не должны превышать допускаемые.
Расчет сводится к удовлетворению условия, по которому контактные напряжения зубьев не должны превышать допускаемые.
В отличие от неподвижного контакта в соединениях, происходящего обычно по большой номинальной площади, контакт при перекатывании в передачах и опорах качения происходит по малым площадкам (начальный контакт по линии или в точке), на которых возникают большие напряжения.
При сжатии цилиндров вдоль образующих (начальное касание по линии – линейчатый контакт) площадка контакта имеет вид полоски и контактные напряжения распределяются по ее ширине по эллипсу.
Контактное напряжение (наибольшее по ширине площадки):
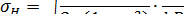
для тел, выполненных из стали и других материалов с коэффициентом Пауссона υ = 0,3
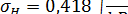
где F — сила прижатия одного тела к другому; Е — приведенный модуль упругости; при изготовлении контактирующих тел из разных материалов:

b – длина контакта; 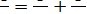 – приведенная кривизна (для тела с внутренним контактом радиус принимается отрицательным, для плоскости R = ∞).
– приведенная кривизна (для тела с внутренним контактом радиус принимается отрицательным, для плоскости R = ∞).
Эту же формулу применяют как приближенную для сжатия вдоль образующих конусов и торов с одинаковыми радиусами образующих. Радиусы R1 и R2 (рисунок 3.10) измеряют по нормали к поверхности.
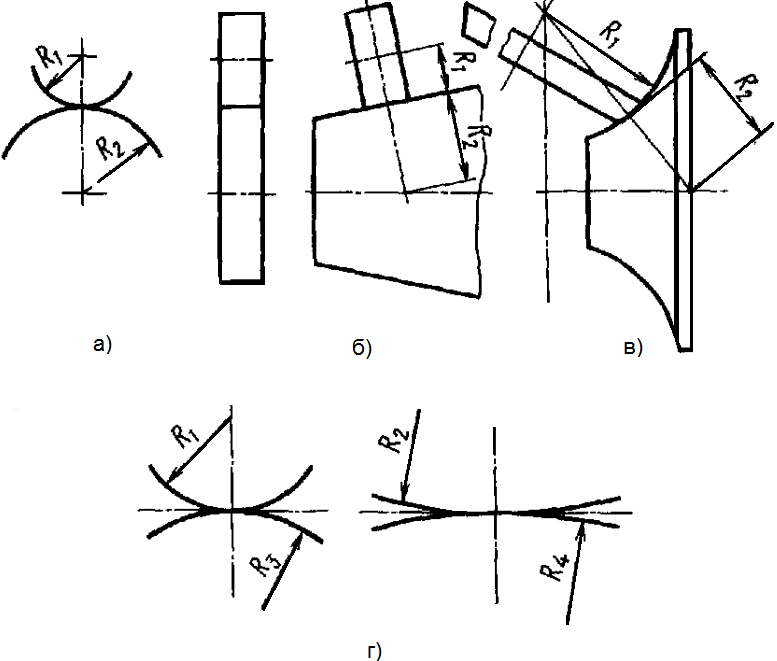
а, б, в – начальное касание по линии; г – начальное касание по точке
Рисунок 3.10 – Расчетные схемы
При сжатии шаров, торов с неодинаковыми радиусами образующих, а также цилиндров и конусов с перекрещивающимися осями (начальное касание в точке – точечный контакт) площадка контакта имеет форму круга или эллипса, а эпюра напряжения соответственно — полусферы или полуэллипсоида.
Контактное напряжение:
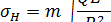
где 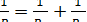 – приведенная кривизна приведенная кривизна в плоскости наиболее тесного контакта (рисунок 3.10); m – коэффициент, зависящий от отношения главных кривизн (рисунок 3.11):
– приведенная кривизна приведенная кривизна в плоскости наиболее тесного контакта (рисунок 3.10); m – коэффициент, зависящий от отношения главных кривизн (рисунок 3.11):

R1 и R2 — главные радиусы кривизны одного тела; R3 и R4 - другого тела.
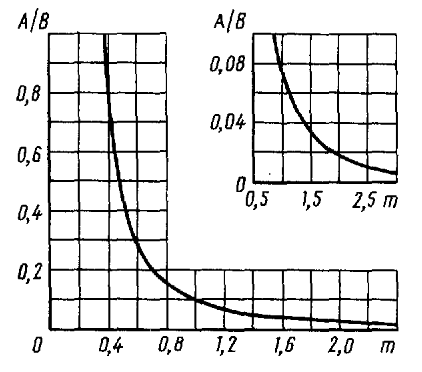
Рисунок 3.11 – График для определения коэффициента m
Как видно из приведенных формул Герца, контактные напряжения пропорциональны нагрузке не в первой степени, а в степени 1/2 или 1/3, а также зависят от модуля упругости. Это связано с тем, что сама площадка контакта растет с ростом нагрузки и зависит от модуля упругости.
Условия применимости формул Герца – незначительные размеры (для полоски – её ширина) площадки контакта по сравнению с радиусами кривизны поверхностей в зоне контакта; контактирующие поверхности идеальные, абсолютно гладкие и сухие, а силы трения отсутствуют; материалы тел анизотропны; деформации только упругие.
В качестве исходной принимают формулу Герца для наибольших контактных напряжений 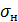 (МПа) при сжатии цилиндров, соприкасающихся вдоль образующих:
(МПа) при сжатии цилиндров, соприкасающихся вдоль образующих:
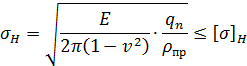
где 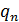 — нормальная к поверхности нагрузка на 1 см, Н/см,
— нормальная к поверхности нагрузка на 1 см, Н/см, 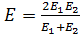 ; - приведенный модуль упругости материала, МПа;
; - приведенный модуль упругости материала, МПа; 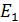 и
и 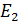 — модули упругости материала шестерни и колеса; если материалы шестерни и колеса одинаковы, то
— модули упругости материала шестерни и колеса; если материалы шестерни и колеса одинаковы, то 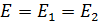 , υ — коэффициент поперечного сжатия;
, υ — коэффициент поперечного сжатия; 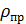 — приведенный радиус кривизны
— приведенный радиус кривизны 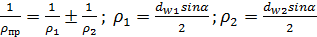 ‒ радиусы кривизны профилей зубьев шестерни и соответственно колеса; знак плюс для внешнего, знак минус для внутреннего зацепления, для рейки
‒ радиусы кривизны профилей зубьев шестерни и соответственно колеса; знак плюс для внешнего, знак минус для внутреннего зацепления, для рейки 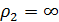 и
и 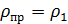 .
.
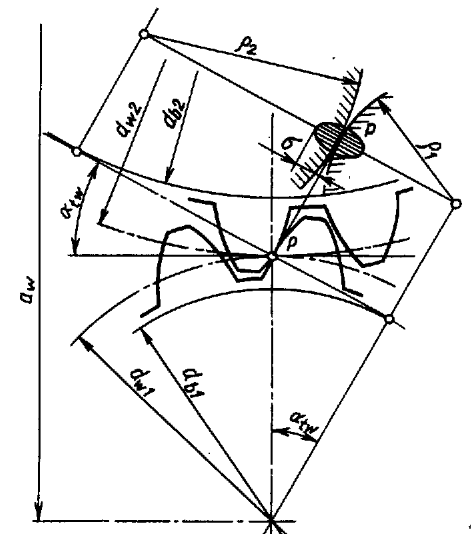
Рисунок 3.12 - Схема к расчету контактной прочности зубьев
Вначале рассматриваем передачу без коррекции. Подставляя в формулу для 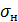 значение
значение 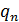 ,
, 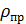 и
и 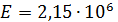 после преобразования получаем расчетную зависимость:
после преобразования получаем расчетную зависимость:
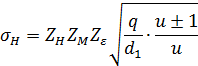
где 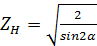 — коэффициент, учитывающий форму соприкасающихся поверхностей, при α = 20°
— коэффициент, учитывающий форму соприкасающихся поверхностей, при α = 20° 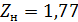 ;
; 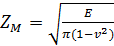 ‒ коэффициент, учитывающий механические свойства материалов колес. В формулах здесь и далее знак плюс соответствует наружному, а знак минус — внутреннему зацеплению.
‒ коэффициент, учитывающий механические свойства материалов колес. В формулах здесь и далее знак плюс соответствует наружному, а знак минус — внутреннему зацеплению. 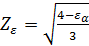 ‒ коэффициент, учитывающий влияние коэффициента торцового перекрытия
‒ коэффициент, учитывающий влияние коэффициента торцового перекрытия 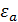 . При отсутствии необходимости повышенной точности расчетов можно принимать
. При отсутствии необходимости повышенной точности расчетов можно принимать 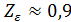 , что соответствует
, что соответствует 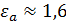 .
.
Дата добавления: 2015-02-05; просмотров: 1569;
