Расчет на прочность при изгибе
1. Расчетом определяют напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого колеса.
Выносливость зубьев, необходимая для предотвращения усталостного излома зубьев, устанавливают сопоставлением расчетного местного напряжения от изгиба в опасном сечении и допускаемого напряжения σF ≤ σFP.
Расчетное местное напряжение при изгибе определяют по формуле:
σF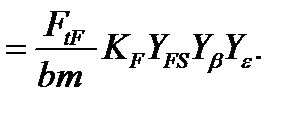 
Для коэффициента нагрузки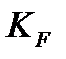 
принимают: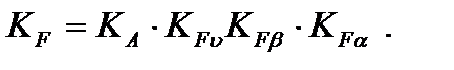 
Между допускаемым напряжением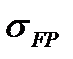 
пределом выносливости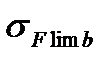 
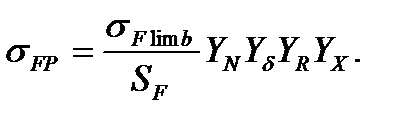
2. Расчет ведут по расчетной окружной силе, отнесенной к единице ширины венца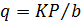 
, где 
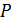— полезная окружная сила на начальном цилиндре; 
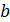— ширина венца; 
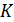— коэффициент нагрузки, учитывающий дополнительные вредные нагрузки, сопутствующие работе передач.
В процессе зацепления точка приложения силы взаимодействия между зубьями перемещается по рабочей части профиля. Принимаем, что силы трения на зубьях малы. Тогда силу взаимодействия (рисунок 3.9) можно считать направленной по нормали к профилям, т. е. по линии зацепления, касательной к основной окружности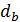 
.
Из геометрических параметров передачи прочность на изгиб прежде всего определяется модулем и шириной колеса.
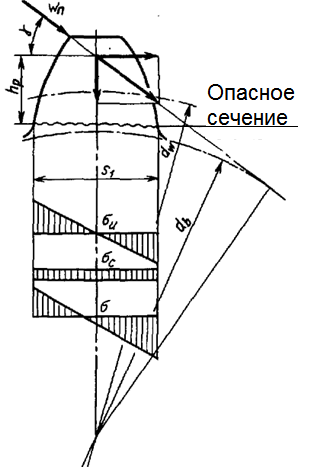
Рисунок 3.9 - Схема к расчету зубьев на изгиб
Проектный расчет зубчатых колес на изгиб обычно производят в форме определения модуля по выбранным числам зубьев или в форме определения модуля по межосевому расстоянию и ширине, определенным из расчетов на контактную прочность.
Если прочность на изгиб является основным критерием работоспособности (для закаленных до высокой твердости зубчатых колес), а числа зубьев передачи заранее заданы кинематическим расчетом (например, согласно условиям точного передаточного отношения в металлорежущих станках и т. д.), а также для открытых передач расчет ведется в форме определения модуля по заданным числам зубьев с последующей проверкой контактной прочности.
Тогда, выразив в предыдущей формуле ширину колес через модуль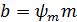 
, получим:
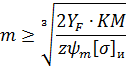
где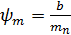 
или принимают равным для прямозубых колес 6…10, для косозубых – 10…25.
Если материал колес одинаковый, то расчет ведут по шестерне, которая имеет более тонкий зуб у основания и, следовательно, большие значения коэффициента прочности зубьев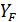 
. Если материал шестерни более прочен, чем материал колеса (что обычно бывает при больших передаточных числах), то расчет ведут по тому из зубчатых колес, у которого меньше отношение 
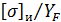. Целесообразно, чтобы 
.
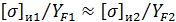Наиболее рациональной формой расчетов, позволяющей обеспечить или приблизиться к равнопрочности зубьев по выкрашиванию и излому, является определение модуля по известному межосевому расстоянию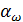 
и ширине колес 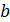, полученным из расчетов на контактную прочность.
Выразим напряжения изгиба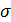 
в зубьях шестерни или колеса через межосевое расстояние 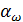, подставив вместо 
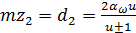, где знак плюс для внешнего, а знак минус для внутреннего зацепления. Здесь и ниже под 
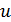понимают передаточное число зубчатой передачи, всегда больше единицы (или равное единице).
Тогда:
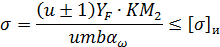
Отсюда минимальное значение модуля:
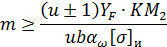
Дата добавления: 2015-02-05; просмотров: 1311;