Приклади розрахунків. Приклад 7.1. Для рами (рис.7.7,а) побудувати епюри згинальних моментів і виконати всі необхідні перевірки розрахунку за умови

Приклад 7.1. Для рами (рис.7.7,а) побудувати епюри згинальних моментів і виконати всі необхідні перевірки розрахунку за умови, що жорсткості всіх елементів рами однакові і рівні EI.

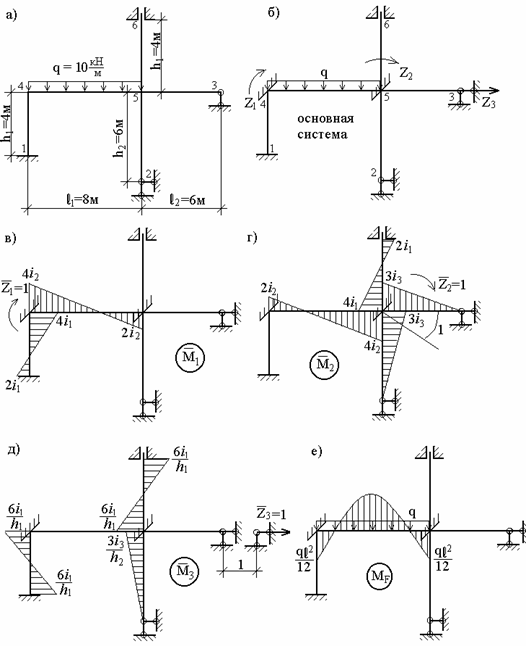
Рис.7.7. До прикладу 7.1

Визначимо число основних невідомих – ступінь кінематичної невизначеності рами. Тому що число невідомих кутових переміщень дорівнює числу жорстких вузлів рами, то n_y = 2. Число незалежних лінійних зсувів n_л = 1. Дійсно, вузли рами 4 і 5 не можуть переміщатися по вертикалі через опорні закріплення 1 і 2 і прийнята гіпотеза про нерозтяжність стержнів і незмінності їх довжини при вигині. Для них можливо тільки горизонтальне переміщення, що буде однаковим для вузлів 4, 5 і 3 унаслідок того, що вони зв'язані між собою стержнями 4-5 і 5-3. Таким чином, ступінь кінематичної невизначеності рами

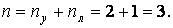
Утворимо основну систему, ввівши зв'язки, що перешкоджають кутовим і лінійним зсувам, і позначимо передбачувані напрямки (довільно) трьох невідомих переміщень (рис.7.7,б). Використовуючи приведену вище допоміжну таблицю методу переміщень, побудуємо епюри згинальних моментів 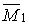, , 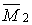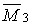від одиничних переміщень уведених зв'язків по заданих напрямках і епюру 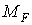від дії навантаження на основну систему (рис.7.7,в-е). Для зручності на цих малюнках використані наступні позначення:

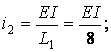
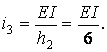
При побудові всіх зазначених епюр потрібно чітко уявляти собі переміщення осі кожного стержня, викликана заданим одиничним зсувом; це дозволить установити положення стиснутих волокон елементів рами і правильно зобразити епюри моментів.

Система канонічних рівнянь має вигляд

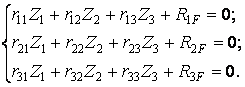
Для визначення коефіцієнтів і вільних членів цих рівнянь, що являють собою реактивні зусилля в накладених зв'язках, застосуємо статичний спосіб. Для цього виражаємо спочатку вузол 4 і розглянемо умови його рівноваги у випадках, представлених на рис.7.7,в-е, тобто визначимо коефіцієнти першого рядка канонічних рівнянь.

На рис.7.8,а-г показаний вузол 4 з діючими на нього моментами з боку відкинутих частин рами і реактивних моментів у защемленні (першого зв'язку). З умов рівноваги цього вузла одержимо

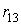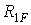Негативний знак у двох останніх випадках пояснюється тим, що напрямки реактивних моментів і протилежні заданому напрямкові кута повороту Z₁ першого зв'язку.

Аналогічно визначимо коефіцієнти другого канонічного рівняння. Для цього виріжемо з рами вузол 5 і розглянемо умови його рівноваги при тих же чотирьох впливах на основну систему (рис.7.8,в-е).

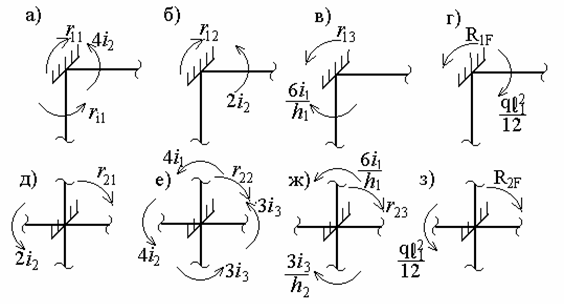
Рис.7.8. Статичний спосіб визначення коефіцієнтів

З рис.56,д-з випливає

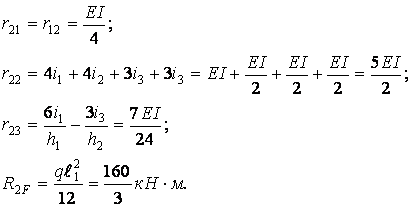
Для визначення коефіцієнтів третього рівняння, що представляють собою реакції у введеному стержні (третього зв'язку), розсічемо стійки рами і розглянемо умови рівноваги її середньої частини, що містить уведений стержень (рис.7.9,а-г). При цьому під умовою рівноваги будемо розуміти рівність нулеві суми проекцій усіх сил, прикладених до виділеної частини рами, на горизонтальну вісь: Відмінні від нуля проекції дадуть шукані реакції у введеному стержні і поперечні сили, прикладені в місцях розсічення стійок і визначаємі по епюрах 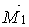, , 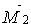, 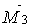M_F.

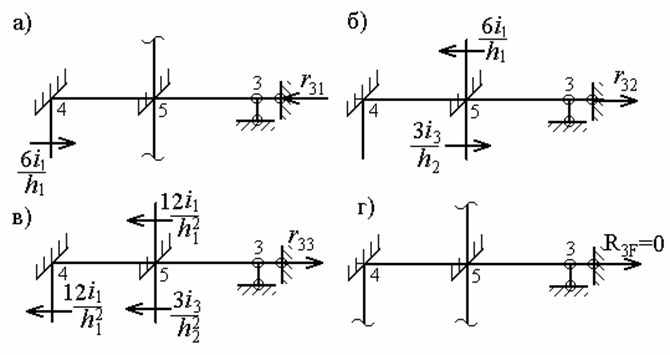
Рис.7.9. Визначення коефіцієнтів методом перетинів

З рис.7.9,а-г випливає

Перевірку обчислених коефіцієнтів і вільних членів можна здійснити способом перемноження епюр. Для виконання універсальної перевірки побудуємо сумарну одиничну епюру згинальних моментів 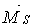, що представляє собою суму одиничних епюр 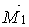, , 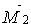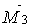(рис.7.10,а) і перемножимо її саму на себе:

Сума коефіцієнтів при невідомих складає

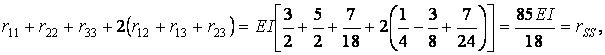
тобто коефіцієнти обчислені правильно.

Для перевірки вільних членів канонічних рівнянь необхідно побудувати епюри згинальних моментів 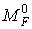від зовнішнього навантаження, прикладеного в будь-якій статично визначній системі, утвореній з заданої рами, і перемножити її з епюрою :

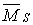Два можливих варіанти епюри 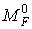представлені на рис.7.10,б,в (можливі й інші варіанти статично визначних рам, утворених із заданої, і, відповідно, інші варіанти епюри 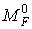). Легко переконатися, що результат перемножування кожної з цих епюр на епюру 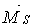дорівнює нулеві, що також підтверджує правильність обчислень, тому що в розглянутому прикладі

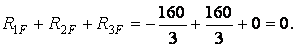
Підставляючи знайдені значення коефіцієнтів і вільних членів у вихідну систему канонічних рівнянь, одержимо

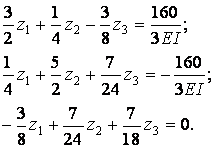
(7.17)

Розв’язок системи (7.17) дає наступні значення невідомих:

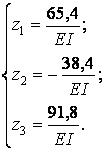
Одиничні епюри моментів (мал.7.7,в-д) тепер можна "виправити", тобто помножити на відповідні значення невідомих. При цьому друга епюра 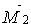поміняє знаки, тому що z₂ < 0. Остаточну епюру згинальних моментів М (рис.7.10,г) побудуємо відповідно до виразу

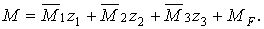
(7.18)

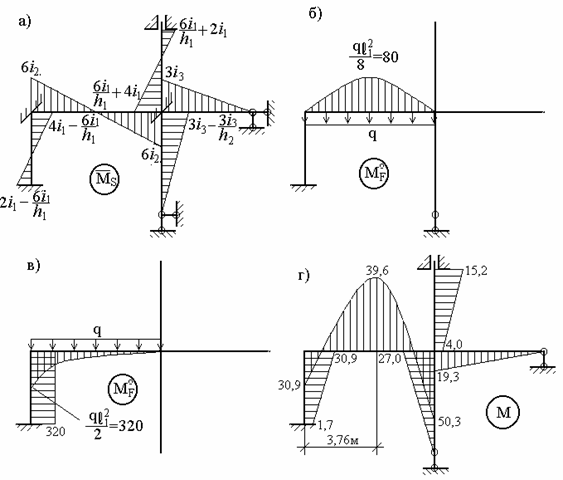
Рис.7.10. Сумарна одинична і остаточна епюри моментів

Виконаємо статичну перевірку. Для цього виражаємо вузли 4 і 5, а також середню частину рами (мал.7.11,а-в) і переконаємося у виконанні умов рівноваги.

Як уже говорилося, статична перевірка є достатнім критерієм правильності виконаного розрахунку. Проте, виконаємо додатково кінематичну перевірку. Для цього побудуємо сумарну одиничну епюру 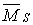в основній системі методу сил (рис.7.11,г). Читачеві надається можливість самостійно переконатися в тому, що результат множення цієї епюри на остаточну епюру моментів М (рис.7.10,г) дорівнює нулеві.

На закінчення відзначимо, що ступінь статичної невизначеності розглянутої рами дорівнює п'яти, а це означає, що трудомісткість розрахунку даної системи методом сил значно вища, ніж при використанні методу переміщень.

Рис.7.11. Статична перевірка (до прикладу 7.1)

Приклад 7.2. Для рами з похилими стійками ( рис.7.12,а) побудувати епюри M, Q, N за умови, що жорсткість ригеля (2-3) у два рази більша, ніж жорсткість похилих стійок 1-2 і 3-4.

Визначаємо ступінь кінематичної невизначеності рами:

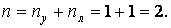
Основну систему утворимо шляхом введення защемлення у вузлі 2 і горизонтального опорного стержня у вузлі 3 (рис.7.12,б).

Для визначення невідомих переміщень Z₁ і Z₂ по напрямках введених зв'язків запишемо систему канонічних рівнянь методу переміщень:

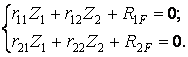
(7.19)

Використовуючи допоміжну таблицю методу переміщень, побудуємо епюри згинальних моментів від одиничного кута повороту 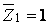і від зовнішнього навантаження (рис.7.12,в,г).

Відзначимо, що вузлове навантаження 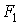не викликає згинальних моментів в основній системі. Для побудови епюри моментів від одиничного горизонтального переміщення 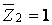другого зв'язку необхідно знати, як переміщаються в цьому випадку кінці стержнів рами. Переміщення вузла 3 відбувається по напрямку, перпендикулярному лінії 3-4 (шукане переміщення 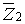є горизонтальною проекцією повного зсуву вузла 3), а вузла 2 — по напрямку, перпендикулярному лінії 1-2. У результаті цього відбувається відносне переміщення вузлів 2 і 3 по вертикалі.

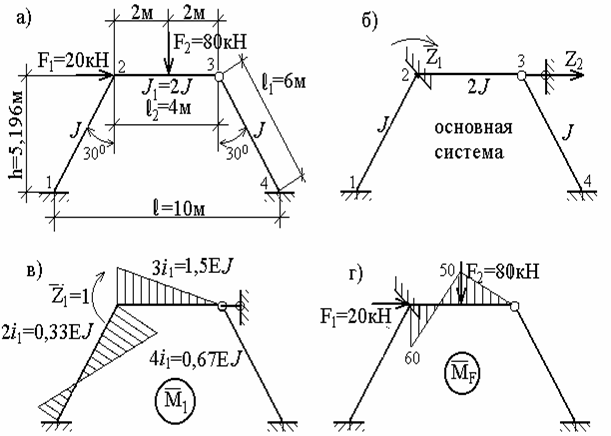
Рис.7.12. Рама з похилими стійками (приклад 7.2)

Для визначення зазначених переміщень побудуємо для шарнірної схеми, утвореної з заданої рами (рис.7.13,а), полярний план переміщень (рис.7.13,б). З цього плану визначимо взаємне переміщення кінців стержнів:

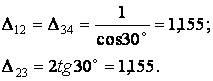
Тому що введене защемлення перешкоджає поворотові вузла 2, то від знайдених взаємних зсувів відбудеться вигин стержнів (рис.7.13,в). Епюра моментів 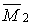може бути тепер побудована за допомогою допоміжної таблиці методу переміщень (рис.7.13,г).

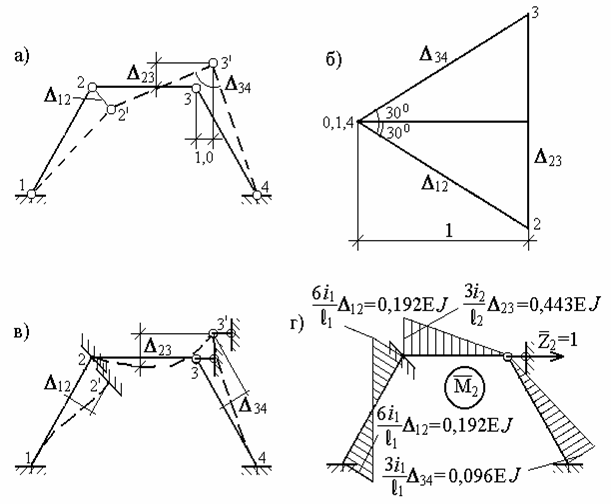
Рис.7.13. До прикладу 7.2

Коефіцієнти r₁₁, r₁₂ і вільний член R_1F визначимо з умови рівноваги вузла 2:

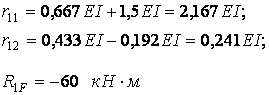
Для визначення коефіцієнта 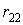, що представляє собою реакцію у введеному стержні від одиничного зсуву 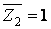, розглянемо умови рівноваги ригеля, відсіченого від стійок. Для цього необхідно визначити поперечні і повздовжні сили, що відповідають епюрі 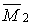, вирізуючи з рами спочатку вузол 2, а потім вузол 3. Так, умови рівноваги вузла 2 (рис.7.14,а) дають:

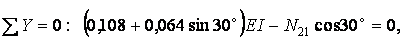
звідки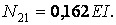

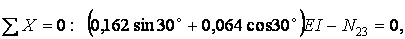
звідки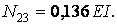

Умови рівноваги вузла 3 (рис.7.14,б) дозволяють одержати:

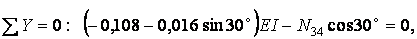
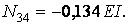
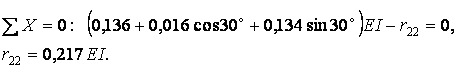
Аналогічно можна визначити і вільний член 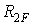по епюрі 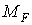, вирізуючи вузли 2 і 3 (рис.7.14,в,г):

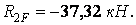
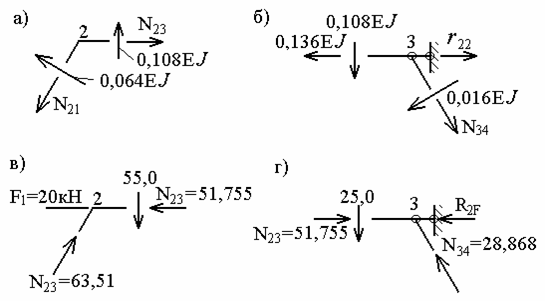
Рис.7.14. Визначення коефіцієнтів шляхом вирізання вузлів

Використання статичного способу для обчислення коефіцієнтів 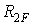і 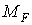для рами з похилими стійками приводить, як можна було переконатися з розглянутого приклада, до ускладнення розрахунків. Тому в подібних випадках доцільно використовувати спосіб перемноження епюр:

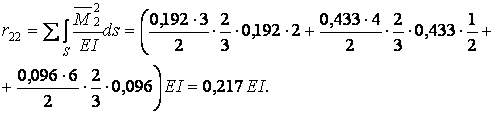
Для визначення вільного члена 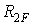способом перемноження епюр потрібно побудувати епюри моментів від зовнішнього навантаження в статично визначеній системі, утвореної з заданої рами (рис.7.15,а):

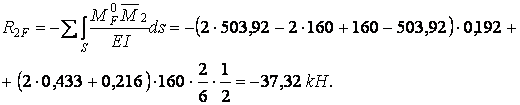
Після підстановки обчислених коефіцієнтів у рівняння (7.19) одержимо

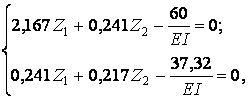
звідки

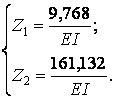
Остаточну епюру моментів (рис.7.15,б) будуємо по формулі

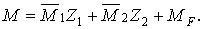
Відповідні їй епюри поперечних і повздовжніх сил показані на рис.7.15,в,г.

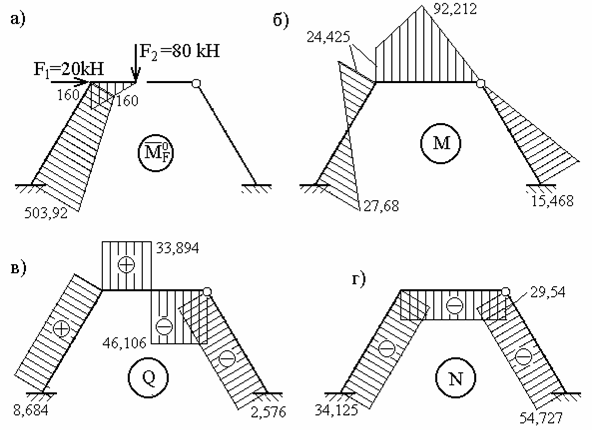
Рис.7.15. Остаточні епюри (до прикладу 7.2)

Можна самостійно переконатися в тому, що для остаточних епюр виконуються статичні перевірки: у вузлі 2 згинальні моменти урівноважені; а сили, що діють на верхню відсічену частину рами, задовольняють умовам рівноваги 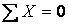і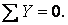

Приклад 7.3. Використовуючи спрощення, зв'язані із симетрією заданої рами (рис.7.16,а), побудувати епюри згинальних моментів, за умови, що жорсткості всіх стержнів однакові і рівні EI.

Ступінь кінематичної невизначеності рами

При виборі основної системи методу переміщень (рис.7.16,б) використовуємо умови симетрії. Згрупуємо невідомі кути повороту, тобто кут повороту вузла 2 представимо у вигляді суми двох кутів повороту 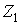і 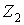, а поворот вузла 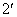, симетричного вузлові 2, — у вигляді різниці кутів 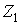і .

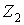Горизонтальне переміщення ригеля 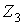є зворотньосиметричним невідомим, тому що вузол 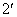при цьому зміщається від осі симетрії рами, а симетричний йому вузол 2 — до осі симетрії.

Для визначення групових невідомих 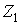, 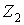і 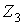запишемо систему трьох канонічних рівнянь методу переміщень:

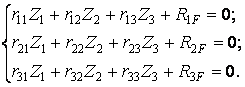
(7.20)

Як видно, форма канонічних рівнянь при групуванні невідомих залишається колишньою. Але всі епюри від одиничних невідомих (рис.7.16, в-д) будуть тільки симетричними або зворотньосиметричними, а канонічні рівняння розпадуться на дві незалежні системи, що містять тільки симетричні або тільки зворотньосиметричні групові невідомі. При цьому невідомі переміщення вузлів, розташованих на осі симетрії, завжди мають симетрію або зворотну симетрію і тому не групуються.

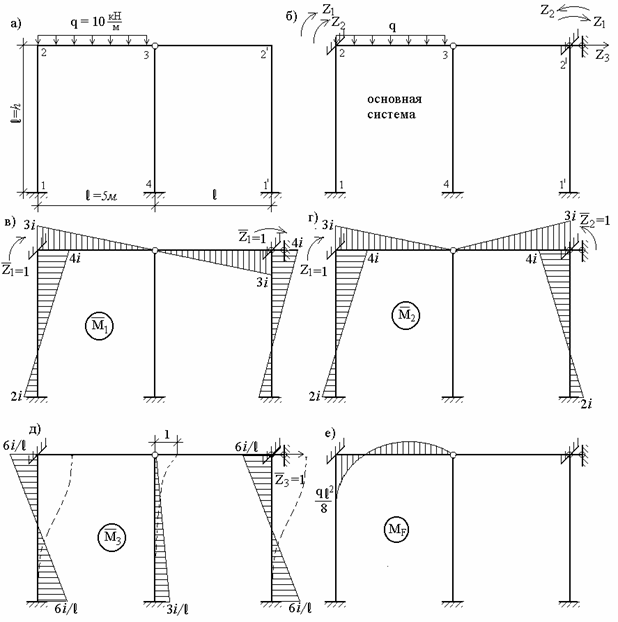
Рис.7.16. Розрахунок рами з урахуванням симетрії (до прикладу 7.3)

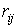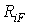Значення одиничних коефіцієнтів і вільних членів у рівняннях (7.20) здобувають трохи інший зміст, ніж раніше. Тут і — узагальнені реакції, що відповідають узагальненому переміщенню 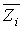від парного зсуву і від зовнішнього навантаження. Ці узагальнені реакції визначаються як алгебраїчні суми простих реакцій у зв'язках, що одночасно зміщаються при груповому парному переміщенні 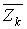. Позитивні напрямки простих реакцій приймаються, як і раніше, такими, що збігаються з напрямками переміщень, які задаються, тих зв'язків, у яких вони визначаються.

При використанні статичного способу для коефіцієнтів і вільних членів канонічних рівнянь (7.20) одержимо

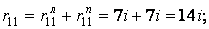
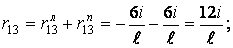
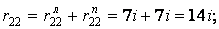
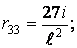
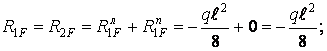
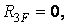
де індексами "л" і "n" позначені відповідно ліва (вузол 2) і права (вузол 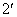) додаткові затиснення, у яких визначаються звичайні реакції (реактивні моменти). Реакції в додатковому стержн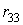і ( і 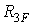) визначені з умови рівноваги 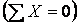відсіченого ригеля рами.

Унаслідок рівності нулеві чотирьох коефіцієнтів система канонічних рівнянь (7.20) розпадається на дві системи, а точніше – на систему рівнянь щодо невідомих Z₁ і Z₃ і рівняння відносно Z₂:

У результаті розв’язання одержимо наступні значення невідомих:

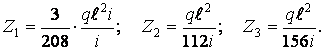
У цьому прикладі позначено

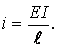
Остаточна епюра моментів (рис.65) має вигляд:

Рис.7.17. Остаточна епюра моментів (до прикладу 7.3)