ДВОХШАРНИРНА АРКА

Статично невизначені арки, як і трьохшарнирні арки, розглянуті в першому розділі, ставляться до розпірних систем. У будівництві застосовуються в основному два види статично невизначених арок: двохшарнирні й бесшарнирні. Двохшарнирною аркою називається криволінійний брус на двох шарнирно-нерухомих опорах. Арка із затисненими кінцями, що не має проміжних шарнірів, називається бесшарнирною аркою. Застосовують їх при будівництві мостів і перекриттів будинків великих прольотів. Розрахунок двохшарнирних і безшарнірних арок виконують методом сил.

Двохшарнирні арки один раз статично невизначені. Як основна система звичайно приймають криволінійну балку (рис. 9.1) із заміною однієї з нерухомих опор рухомою. За зайве невідоме приймають розпір .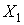

Для визначення розпору 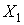становлять канонічне рівняння

,

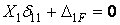звідки

.

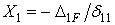Переміщення 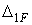й визначають, використовуючи формулу Мору:

;

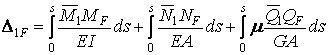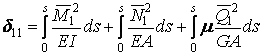
Інтегрування проводять по довжині осі арки з урахуванням змінності перетину арки.

При розрахунку арок, найбільше часто застосовуваних у будівництві, зі стрілою підйому 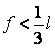й висотою перетину 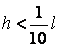можна при визначенні зневажити впливом поперечних сил, а при визначенні 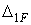— впливом і поперечних і поздовжніх сил. Тому можна прийняти

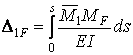;	(9.1)
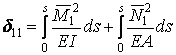.	(9.2)

а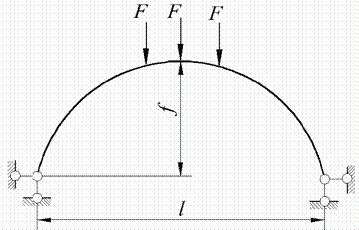
б
в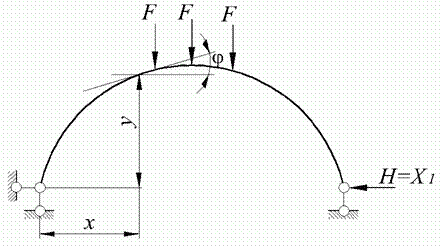

Рис. 9.1. Двохшарнірна арка

Порівняльними підрахунками встановлено, що пр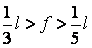и й 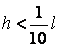при визначенні можна зневажити не тільки поперечними силами, але й поздовжніми. У цьому випадку

.

Беручи до уваги, що (рис. 9.1, в), одержимо:

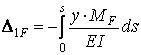;	(9.3)
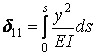.	(9.4)

Якщо вираз 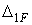й 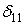інтегрувати важко або неможливо, застосовують чисельне інтегрування.

Моменти, поперечні і поздовжні сили визначають так само, як і для трьохшарнірних арок.

Згинальний момент у будь-якому перетині (рис. 9.1, в)

;

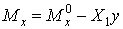поперечна сила

;

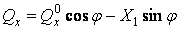поздовжня сила

.

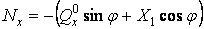Приклад 9.1.Розрахувати двохшарнирну арку, навантажену рівномірно розподіленим навантаженням на половині прольоту (рис. 9.2, а). Арка має постійний перетин. Основна система показана на рис. 9.2, б.

Рівняння осі арки .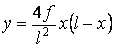

Напишемо канонічне рівняння методу сил:

.

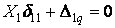а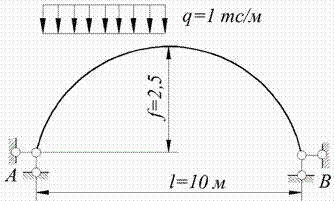
б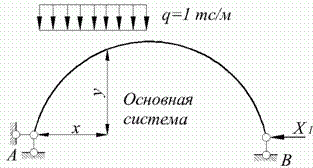
в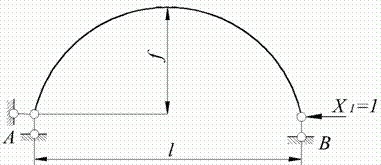
г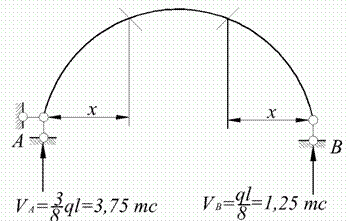
д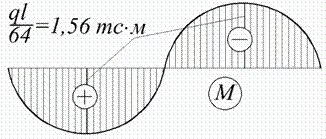

Рис. 9.2. Наприклад 9.1

Для визначення переміщень розглянемо окремо випадки дії сили 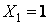й зовнішнього навантаження (рис. 9.2, в, г).

Так як арка постійного перетину й досить полога, то можна прийняти 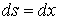, тоді

; .

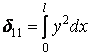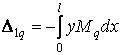Обчислимо переміщення :

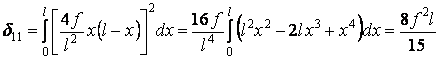
Для обчислення 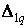складемо два інтеграли: один для лівої половини від 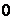до 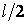й іншої для правої — від до (приймаючи початок координат на правій опорі).

Опорні реакції:

; .

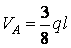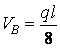Момент від навантаження в лівій половині арки

;

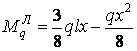у правої

.

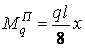У такий спосіб

Підставимо вираз й 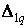у канонічне рівняння:

.

Звідси

.

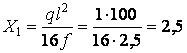Тепер визначимо згинальні моменти 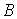лівої частини арки

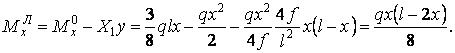
У правій частині

.

Епюра згинальних моментів показана на рис. 9.2, д.