Рішення. Так само, як і в попередньому прикладі, осі і є осями зворотної симетрії щодо зовнішніх сил
Так само, як і в попередньому прикладі, осі  і
і 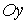 є осями зворотної симетрії щодо зовнішніх сил
є осями зворотної симетрії щодо зовнішніх сил 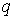 . Тому в перетинах, проведених через крапки
. Тому в перетинах, проведених через крапки 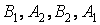 , будуть діяти лише поперечні сили. З умов рівноваги чверті кільця (мал. 9.12, б) у крапках
, будуть діяти лише поперечні сили. З умов рівноваги чверті кільця (мал. 9.12, б) у крапках 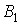 і
і 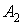 знаходимо однакові за значенням поперечні сили:
знаходимо однакові за значенням поперечні сили:
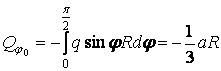 .
.
Отже, у довільному перетині кільця, обумовленому кутом 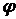 ,
,
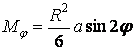 ;
; 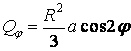 ;
; 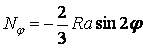
Приклад 9.5. Кільце навантажене (рис. 9.13, а) з радіальним навантаженням 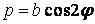 , де
, де 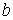 — амплітуда навантаження. У даному прикладі осі
— амплітуда навантаження. У даному прикладі осі 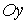 і
і  є осями симетрії. Тому в крапках
є осями симетрії. Тому в крапках 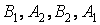 повинні діяти симетричні сили, якими є осьові зусилля
повинні діяти симетричні сили, якими є осьові зусилля 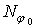 й згинальні моменти
й згинальні моменти 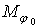 .
.
| а | 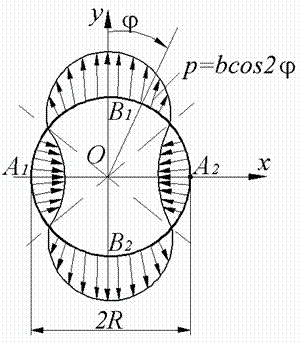
| б | 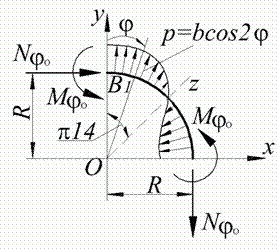
|
Рис. 9.13. Наприклад 9.5
Розглянемо рівновагу чверті кільця (рис. 9.13,б). Внаслідок зворотної симетрії системи щодо 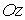 осі в точках
осі в точках 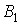 і
і 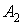 повинні діяти однакові за значенням, але різні за знаком внутрішні зусилля.
повинні діяти однакові за значенням, але різні за знаком внутрішні зусилля.
Проектуючи всі сили на вісь 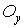 , одержимо
, одержимо
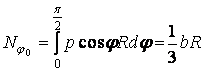 .
.
Якщо взяти момент всіх сил чверті кільця відносно початку координат — точки 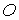 , то одержимо
, то одержимо
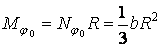 .
.
Тепер можна легко визначити внутрішні зусилля для довільного перетину:
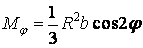 ;
; 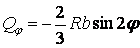 ;
; 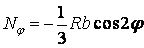
Визначимо радіального 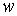 й
й 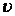 кільцеві й переміщення окремих крапок периметра кільця. Позитивними будемо вважати напрямку переміщень
кільцеві й переміщення окремих крапок периметра кільця. Позитивними будемо вважати напрямку переміщень 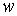 від центра, а
від центра, а 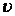 — по ходу збільшення кута
— по ходу збільшення кута 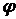 , тобто за годинниковою стрілкою.
, тобто за годинниковою стрілкою.
Формули для визначення цих переміщень мають вигляд:
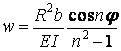 ; ;
| (9.7) |
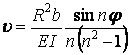 , ,
| (9.8) |
де 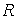 — радіус кільця;
— радіус кільця; 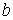 — амплітудне значення навантаження.
— амплітудне значення навантаження.
При визначенні переміщень необхідно знати загальне вираження для згинальних моментів 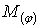 .
.
У табл. 9.2 наведені довідкові дані зусиль і переміщень для кілець, навантажених окремими видами зовнішніх з навантажень.
Таблиця 9.2
Довідкові дані зусиль і переміщень для кілець
Навантаження
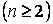
| Зусилля | Переміщення | ||||
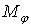
| 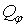
| 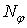
| радіальні
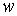
| кільцеві
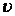
| ||
| Радіальна | 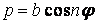
| 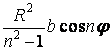
| 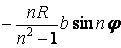
| 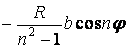
| 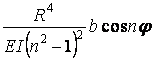
| 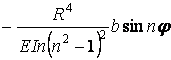
|
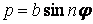
| 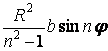
| 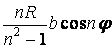
| 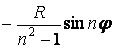
| 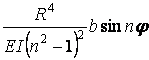
| 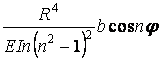
| |
| Кільцева | 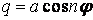
| 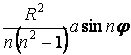
| 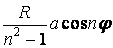
| 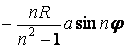
| 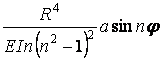
| 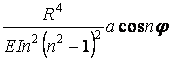
|
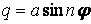
| 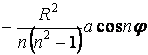
| 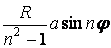
| 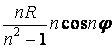
| 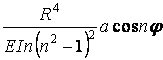
| 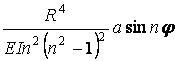
|
Дата добавления: 2015-01-29; просмотров: 751;
