Приклади розрахунків. Приклад 5.1. Визначити прогин у середині прольоту і кут повороту лівого опорного перетину балки, навантаженої рівномірно розподіленим навантаженням

Приклад 5.1. Визначити прогин у середині прольоту і кут повороту лівого опорного перетину балки, навантаженої рівномірно розподіленим навантаженням (мал.5.7,а), методом Мора.

Розглянемо три стани балки: перше (вантажне) — при дії заданого розподіленого навантаження 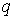; йому відповідає епюра моментів 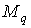(мал.5.7,б). Другий стан (одиничне) — при дії зосередженої сили 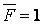, прикладеної в точці 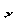; йому відповідає епюра моментів 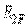(мал.5.7,в). Третій стан (також одиничне) — при дії зосередженого моменту 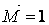, прикладеного в точці 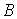; йому відповідає епюра моментів 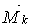(мал.5.7,г). Приймемо початок координат на лівій опорі; тоді ординати зазначених епюр у перетині з координатою 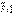відповідно рівні

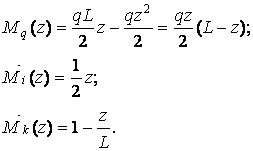
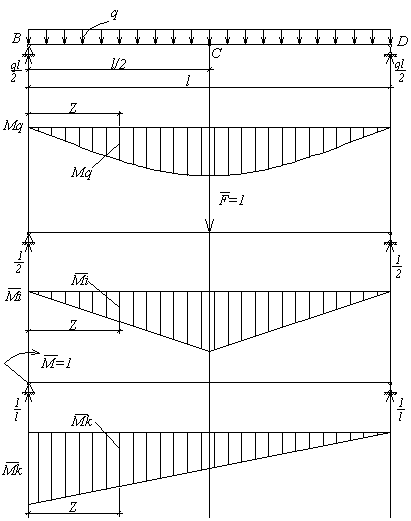
Рис.5.7. До прикладу 5.1

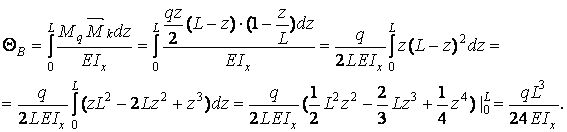
Обчислюємо прогин балки в точці :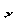

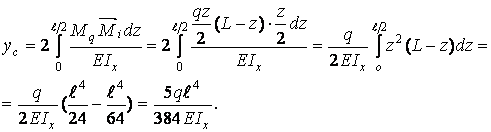
Знак "+" означає, що точка 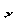переміститься в напрямку дії сили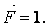

Обчислюємо кут повороту перетину :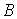

Приклад 5.2. Визначити прогин балки в середині прольоту (мал.5.8,а) методом Мора. Оцінити вплив поперечної сили на загальну величину прогину.

Розглянемо два стани балки. Перший стан (вантажне) – при дії сили 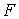(мал.5.8,а); йому відповідають епюри згинальних моментів 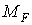(мал.5.8,б) і поперечних сил 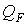(мал.5.8,в).

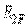Другий стан (одиничне) – при дії сили (мал.5.8,г); йому відповідають епюри згинальних моментів (мал.5.8,д) і поперечних сил 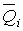(мал.5.8,е).

У зв'язку з відсутністю повздовжніх сил у поперечних перерізах балки інтеграл Мора (5.18) приймає вид

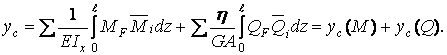
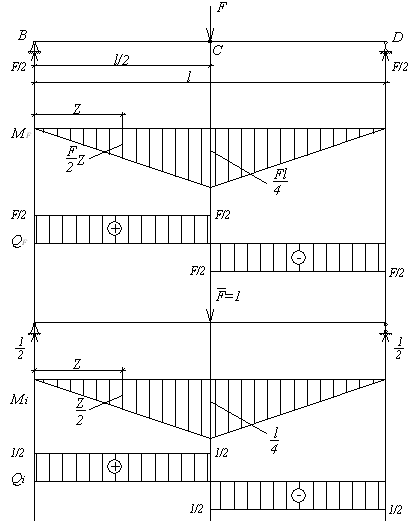
Рис.5.8. До прикладу 5.2

Підставляючи значення згинальних моментів і поперечних сил у перетині з координатою 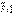(мал.5.8) для складового повного переміщення одержимо

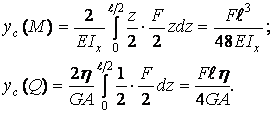
Оцінимо вплив поперечної сили на загальну величину прогину. Нехай розглянута балка має прямокутний поперечний переріз зі сторонами 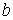і 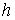, при цьому .

Тоді площа перетину і його осьовий момент інерції рівні:

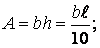
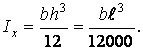
Будемо вважати, що 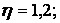тоді

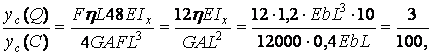
тобто прогин, обумовлений деформацією зрушення, складає 3% від прогину, обумовленого вигином. Легко переконатися, що при збільшенні виразу 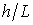вплив поперечних сил на величину прогину стає ще менш значним.