Основні варіанти перемноження епюр

Очевидно, що розмаїтість прикладених навантажень і геометричних схем конструкцій приводить до різних, з погляду геометрії, епюр, що перемножуються. Для реалізації правила Верещагіна потрібно знати площі геометричних фігур і координати їхніх центрів тяжіння. На мал.5.10 представлені деякі основні варіанти, що виникають у практичних розрахунках.

Для перемноження епюр складної форми їх необхідно розбивати на найпростіші. Наприклад, для перемноження двох епюр, що мають вид трапеції, потрібно одну з них розбити на трикутник і прямокутник, помножити площу кожного з них на ординату другої епюри, розташовану під відповідним центром тяжіння, і результати скласти. Аналогічно роблять і для множення криволінійної трапеції на будь-яку лінійну епюрі.

Якщо зазначені вище дії проробити в загальному виді, то одержимо для таких складних випадків формули, зручні для використання в практичних розрахунках (мал.5.11). Так, результат перемноження двох трапецій (мал.5.11,а)

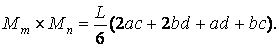
(5.21)

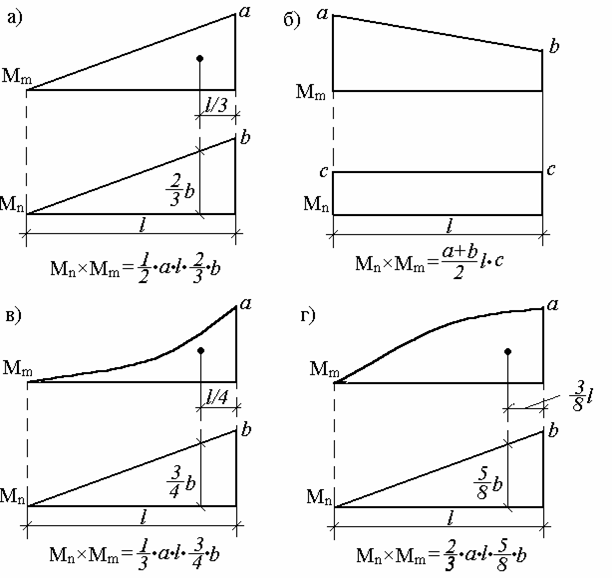
Рис.5.10. Перемноження епюр

По формулі (5.21) можна перемножити й епюри, що мають вид "перекручених" трапецій (мал.5.11,б), але при цьому добуток ординат, розташованих по різні сторони від осей епюр, враховується зі знаком мінус.

Якщо одна з епюр, що перемножуються обкреслена по квадратній параболі (що відповідає навантаженню рівномірно розподіленим навантаженням), то для перемноження з другою (обов'язково лінійною) епюрою її розглядають як суму (мал.5.11,в) або різницю (мал.5.11,г) трапецеїдальної і параболічної епюр. Результат перемноження в обох випадках визначається формулою

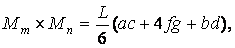
(5.22)

але значення 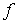при цьому визначається по-різному (мал.5.11, в, г).

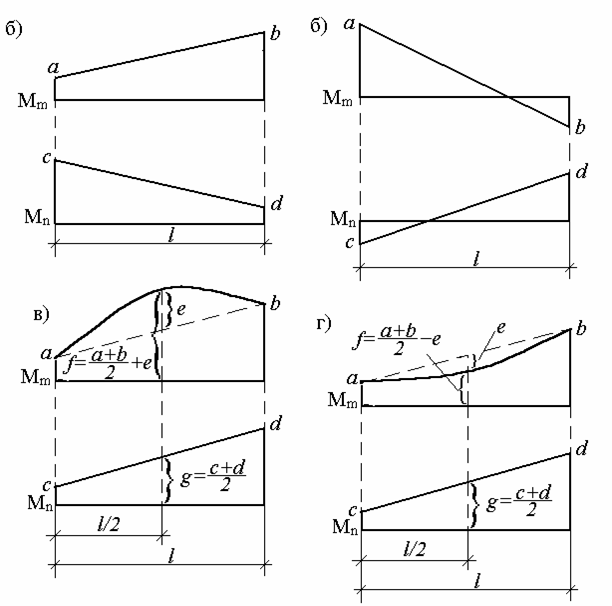
Рис.5.11. Перемноження трапецій

Можливі випадки, коли жодна з епюр, що перемножуються не є прямолінійною, але хоча б одна з них обмежена ламаними прямими лініями. Для перемноження таких епюр їх попередньо розбивають на ділянки, у межах кожної з яких принаймні одна епюра є прямолінійною.

Розглянемо використання правила Верещагіна на конкретних прикладах.

Приклад 5.3. Визначити прогин у середині прольоту і кут повороту лівого опорного перетину балки, навантаженої рівномірно розподіленим навантаженням (мал.5.12,а), способом Верещагіна.

Послідовність розрахунку способом Верещагіна – така ж, як і в методі Мора, тому розглянемо три стани балки: вантажне – при дії розподіленого навантаження ; йому відповідає епюра (мал.5.12,б), і два одиничних стани — при дії сили прикладеної в точці С (епюра 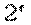, мал.5.12,в), і моменту 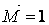, прикладеного в точці В (епюра 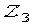, мал.5.12,г).

Прогин балки в середині прольоту

.

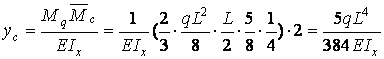Аналогічний результат був отриманий раніше методом Мора (приклад 5.1). Варто звернути увагу на той факт, що перемноження епюр виконувалося для половини балки, а потім, у силу симетрії, результат подвоювався. Якщо ж площу всієї епюри 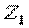помножити на розташовану під її центром тяжіння ординату епюри ( 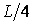на мал.5.12,в), то величина переміщення буде зовсім іншого і неправильною, тому що епюра обмежена ламаною лінією. На неприпустимість такого підходу уже вказувалося вище.

А при обчисленні кута повороту перетину в точці В можна площу епюри 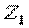помножити на розташовану під її центром тяжіння ординату епюри 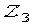( 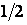, мал.5.12,г), тому що епюра 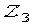обмежена прямою лінією:

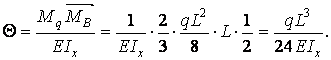
Цей результат також збігається з результатом, отриманим раніше методом Мора (приклад 5.1).

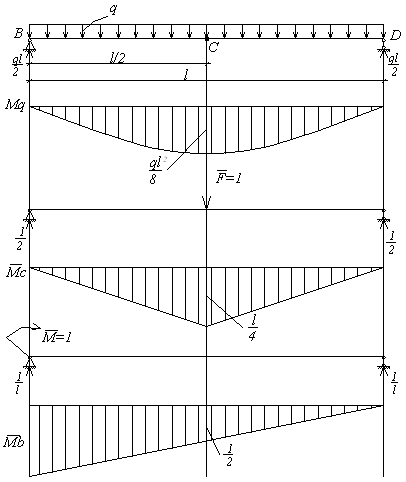
Рис.5.12. До прикладу 5.3

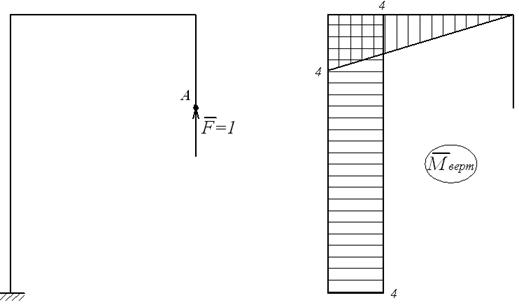
Приклад 5.4. Визначити горизонтальне і вертикальне переміщення точки А в рамі (мал.5.13,а).

Як і в попередньому прикладі, для розв’язання задачі необхідно розглянути три стани рами: вантажне і два одиничних. Епюра моментів M_F, що відповідає першому станові, представлена на мал.5.13,б. Для обчислення горизонтального переміщення прикладаємо в точці А по напрямку шуканого переміщення (тобто горизонтально) силу 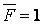, а для обчислення вертикального переміщення силу 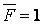прикладаємо вертикально (мал.5.13,в,д). Відповідні епюри 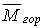і 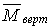показані на мал.5.13,г,е.

а	б
в	г
д	е

Рис.5.13. До прикладу 5.4

Горизонтальне переміщення точки А

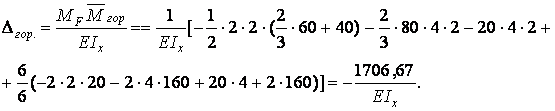
При обчисленні 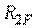на ділянці АВ трапеція (епюра 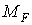) розбита на трикутник і прямокутник, після чого трикутник з епюри 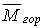помножений на кожну з цих фігур. На ділянці ВР криволінійна трапеція розділена на криволінійний трикутник і прямокутник, а для перемноження епюр на ділянці СД використана формула (5.21).

Знак "-", отриманий при обчисленні 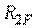, означає, що точка А переміщається по горизонталі не вліво (у цьому напрямку прикладений сила 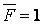), а вправо.

Вертикальне переміщення точки А

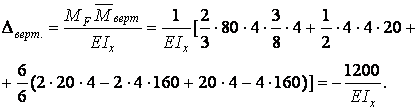
Тут знак " - " означає, що точка А переміщається вниз, а не нагору.

Відзначимо, що одиничні епюри моментів, побудовані від сили 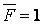, мають розмірність довжини, а одиничні епюри моментів, побудовані від моменту 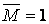, є безрозмірними.

Приклад 5.5. Визначити вертикальне переміщення точки А плоско-просторової системи (мал.5.14,а).

а	б
в	г

Рис.5.14. До прикладу 5.5

Як відомо, у поперечних перерізах стержнів плоско-просторової системи виникають три внутрішніх силових фактори: поперечна сила 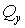, згинальний момент 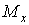і крутний момент 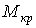. Тому що вплив поперечної сили на величину переміщення незначний, то при обчисленні переміщення методом Мора і Верещагіна із шести доданків залишаються тільки два.

Для розв’язання задачі побудуємо епюри згинальних моментів 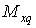і крутних моментів 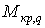, від зовнішнього навантаження (мал.5.14,б), а потім в точці А прикладемо силу 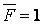по напрямку шуканого переміщення, тобто вертикального (мал.5.14,в), і побудуємо одиничні епюри згинальних моментів 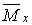і крутних моментів 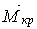, (мал.5.14,г). Стрілками на епюрах крутних моментів, показані напрямки закручування відповідних ділянок плоско-просторової системи.

Вертикальне переміщення точки А

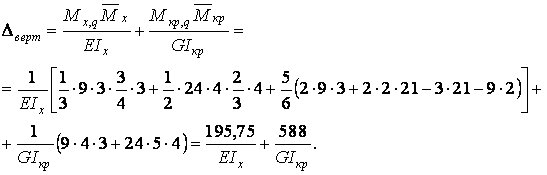
При перемноженні епюр крутних моментів, добуток береться зі знаком "+", якщо стрілки, що вказують напрямок кручення, однаково спрямовані, і зі знаком " - " - у противному випадку.