Правило Верещагіна

Недоліком методу Мора є необхідність одержувати значення внутрішніх силових факторів, що входять у підінтегральний вираз формул (5.18) і (5.19), у загальному виді, як функцій від 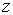, що стає досить трудомістким уже при двох-трьох ділянках розбивки в балках і особливо — у рамах.

Виявляється, що від цього недоліку можна уникнути, якщо безпосереднє інтегрування у формулах Мора замінити так званим перемножуванням епюр. Така заміна можлива в тих випадках, коли хоча б одна з епюр, що перемножуються є прямолінійною. Цій умові відповідають усі системи, що складаються з прямолінійних стержнів. Дійсно, у таких системах епюра, побудована від узагальненої одиничної сили, завжди буде прямолінійною.

Спосіб обчислення інтеграла Мора шляхом заміни безпосереднього інтегрування перемноженням відповідних епюр називається способом (або правилом) Верещагіна і полягає в наступному: щоб перемножити дві епюри, з яких хоча б одна є прямолінійною, потрібно площу однієї епюри (якщо є криволінійна епюра, то обов'язково її площа) помножити на ординату іншої епюри, розташовану під центром тяжіння першої.

Доведемо справедливість цього правила.

Розглянемо дві епюри (мал.5.9). Нехай одна з них ( 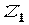) є вантажною і має криволінійний обрис, а друга 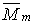відповідає одиничному навантаженню і є лінійною.

З мал.5.9 випливає, що 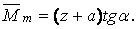Підставимо значення 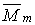у вираз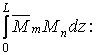

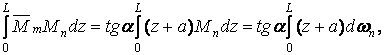
де 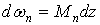— диференціал площі 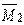епюри .

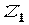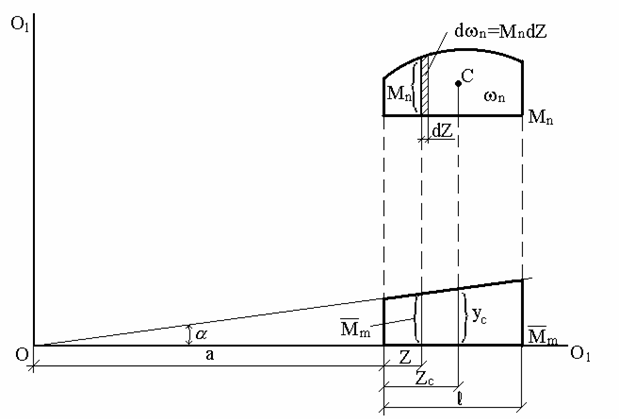
Рис.5.9. Правило Верещагіна

Інтеграл 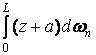являє собою статичний момент площі 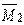щодо осі О – О₁, при цьому

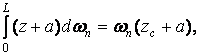
де 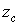— абсциса центра тяжіння площі 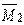, тоді

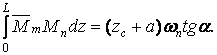
Враховуючи, що 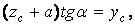одержимо

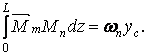
(5.20)

Вираз (5.20) визначає результат перемноження двох епюр, а не переміщення. Щоб одержати переміщення, цей результат потрібно розділити на жорсткість, що відповідає внутрішнім силовим факторам, що знаходяться під знаком інтеграла.