Теорема про взаємність переміщень

Нехай у першому стані до системи прикладена сила 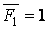, у другому — 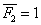(мал.5.5). Позначимо переміщення, викликані одиничними силами (або одиничними моментами 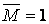) символом 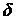. Тоді переміщення розглянутої системи по напрямку одиничної сили 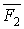в першому стані (тобто викликане силоміць ) — 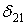, а переміщення по напрямку сили в другому стані — .

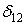На підставі теореми про взаємність робіт 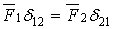, але 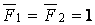, тому 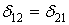, або в загальному випадку дії будь-яких одиничних сил:

.

(5.16)

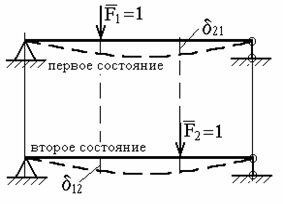
Рис.5.5. До теореми про взаємність переміщень

Отримана рівність (5.16) зветься теореми про взаємність переміщень (або теореми Максвелла): для двох одиничних станів пружної системи переміщення по напрямку першої одиничної сили, викликана другою одиничною силою, дорівнює переміщенню по напрямку другої сили, викликаному першою силою.