Робота зовнішніх сил. Потенційна енергія
Визначимо роботу сили 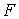 , статично прикладеної до деякої пружної системи (мал.5.1, а), матеріал якої діє за законом Гука.
, статично прикладеної до деякої пружної системи (мал.5.1, а), матеріал якої діє за законом Гука.
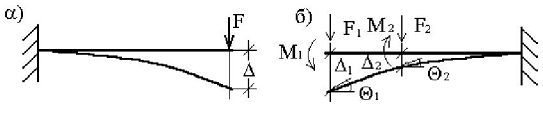
Рис. 5.1. До визначення роботи зовнішніх сил
При малих деформаціях до цієї системи застосуємо принцип незалежності дії сил, отже, переміщення окремих точок і перетинів конструкції прямо пропорційні викликаючому їх навантаженню:
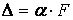 , ,
| (5.2) |
де 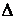 — переміщення по напрямку сили;
— переміщення по напрямку сили; 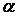 — деякий коефіцієнт, що залежить від матеріалу, схеми і розмірів спорудження. Збільшення сили
— деякий коефіцієнт, що залежить від матеріалу, схеми і розмірів спорудження. Збільшення сили 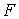 на нескінченно малу величину
на нескінченно малу величину 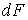 викликає збільшення переміщення на
викликає збільшення переміщення на 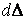 .
.
Складемо вираз елементарної роботи зовнішньої сили на переміщенні 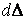 , відкидаючи при цьому нескінченно малі величини другого порядку малості:
, відкидаючи при цьому нескінченно малі величини другого порядку малості: 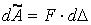 .
.
Замінимо 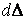 , використовуючи (5.2):
, використовуючи (5.2):
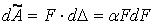 .
.
Інтегруючи цей вираз в межах повної зміни сили від нуля до її кінцевого значення, одержимо формулу для визначення роботи, яка виконується статично прикладеною зовнішньою силою 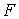 :
:
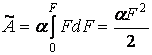
або, з урахуванням (5.2):
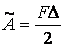 , ,
| (5.3) |
тобто робота зовнішньої сили при статичній дії її на будь-яке пружне спорудження дорівнює половині добутку значення цієї сили на величину відповідних їй переміщення.
Для узагальнення отриманого висновку під силою розуміють будь-яку дію, прикладену до пружної системи, тобто не тільки зосереджену силу, але і момент або рівномірно розподілене навантаження.
Під переміщенням розуміють той його вид, на якому дана сила виконує роботу: зосередженій силі відповідає лінійне переміщення, зосередженому моментові — кутове, рівномірно розподіленій навантаженню — площа епюри переміщень на ділянці дії навантаження.
При статичній дії на конструкцію групи зовнішніх сил робота цих сил дорівнює половині суми добутків кожної сили на величину відповідних їй переміщення, викликаного дією всієї групи сил. Наприклад, при дії на балку (мал.5.1,б) зосереджених сил 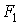 ,
, 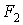 і зосереджених моментів
і зосереджених моментів 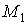 і
і 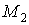 робота зовнішніх сил
робота зовнішніх сил
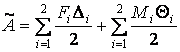 . .
| (5.4) |
Роботу зовнішніх сил на викликаних ними переміщеннях можна виразити й інакше — через внутрішні силові фактори (згинальні моменти, повздовжні і поперечні сили), що виникають у поперечних перерізах системи.
Виділимо з прямолінійного стержня двома перетинами, перпендикулярними його осі (мал.5.2, а), нескінченно малий елемент 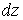 .
.
Стержень складається з нескінченно великого числа таких елементів. До кожного елемента 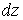 в загальному випадку плоскої задачі прикладені повздовжня сила
в загальному випадку плоскої задачі прикладені повздовжня сила 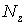 , згинальний момент
, згинальний момент 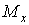 і поперечна сила
і поперечна сила 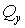 .
.
Для виділеного елемента 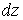 зусилля
зусилля  являються зовнішніми силами, тому роботу
являються зовнішніми силами, тому роботу 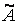 можна одержати як суму робіт, виконаних статично зростаючими зусиллями
можна одержати як суму робіт, виконаних статично зростаючими зусиллями  на відповідних деформаціях елементів
на відповідних деформаціях елементів 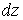 .
.
Розглянемо елемент 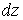 , що знаходиться тільки під дією повздовжніх сил
, що знаходиться тільки під дією повздовжніх сил 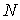 (мал.5.2,б). Якщо його лівий перетин вважати нерухомим, то правий перетин під впливом повздовжньої сили переміститься вправо на величину
(мал.5.2,б). Якщо його лівий перетин вважати нерухомим, то правий перетин під впливом повздовжньої сили переміститься вправо на величину 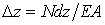 . На цьому переміщенні сила
. На цьому переміщенні сила 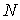 виконає роботу:
виконає роботу:
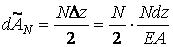 . .
| (5.5) |
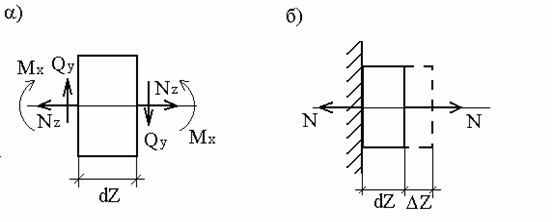
Рис. 5.2. Сили, що діють на нескінченно малий елемент
Якщо нерухомо закріпити лівий перетин елемента  , що знаходиться під дією тільки згинальних моментів
, що знаходиться під дією тільки згинальних моментів 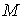 (мал.5.3,а), то взаємний кут повороту торцевих перетинів елемента буде дорівнює кутові повороту
(мал.5.3,а), то взаємний кут повороту торцевих перетинів елемента буде дорівнює кутові повороту 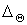 його правого перетину
його правого перетину
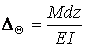 .
.
На цьому переміщенні момент 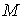 виконає роботу
виконає роботу
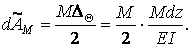
| (5.6) |
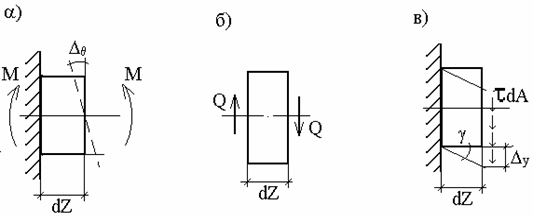
Рис. 5.3. До визначення роботи внутрішніх сил
Закріпимо лівий перетин елемента 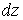 , що знаходиться під дією тільки поперечних сил
, що знаходиться під дією тільки поперечних сил 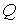 (мал.5.3,б,в), а до правого прикладемо дотичні зусилля
(мал.5.3,б,в), а до правого прикладемо дотичні зусилля 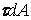 , рівнодіючої яким являється поперечна сила
, рівнодіючої яким являється поперечна сила 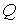 . Припустимо, що дотичні напруження
. Припустимо, що дотичні напруження 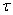 рівномірно розподілені по всій площі
рівномірно розподілені по всій площі 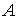 поперечного перерізу, тобто
поперечного перерізу, тобто 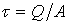 , тоді переміщення
, тоді переміщення 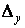 визначаються у виді
визначаються у виді
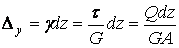 ,
,
а робота сили 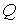 на цьому переміщенні буде
на цьому переміщенні буде
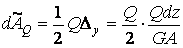
| (5.7) |
У дійсності дотичні напруження 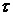 розподілені по площі поперечного перерізу нерівномірно, що враховується введенням у (5.7) поправочного коефіцієнту
розподілені по площі поперечного перерізу нерівномірно, що враховується введенням у (5.7) поправочного коефіцієнту 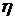 .
.
Підсумовуючи (5.5) – (5.7), одержимо повне значення роботи:
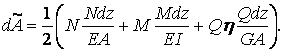
| (5.8) |
Інтегруючи вираз 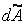 в межах довжини
в межах довжини 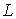 кожної ділянки всіх стержнів і підсумовуючи результати, одержимо
кожної ділянки всіх стержнів і підсумовуючи результати, одержимо
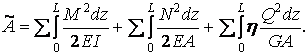
| (5.9) |
З формули (5.9) випливає, що робота зовнішніх сил на викликаних ними переміщеннях завжди позитивна.
На підставі закону збереження енергії робота 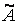 зовнішніх сил переходить у потенційну енергію деформації, тобто
зовнішніх сил переходить у потенційну енергію деформації, тобто 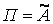 .
.
Дата добавления: 2015-01-29; просмотров: 2238;
