Розв’язання. Обчислюємо опорні реакції:
Обчислюємо опорні реакції:
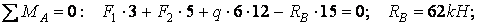
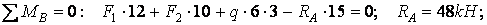

Виконуємо перевірку:
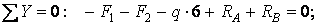
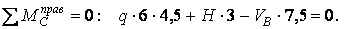
Для побудови епюр розбиваємо арку на ділянки і вибираємо характерні перетини на границях ділянок, а також посередині кожної ділянки (перетину 1 – 9, мал.4.16).
Ординати 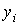 перетинів 1 – 9 обчислюємо по заданому рівнянню осі арки, а диференціюючи це рівняння, одержимо
перетинів 1 – 9 обчислюємо по заданому рівнянню осі арки, а диференціюючи це рівняння, одержимо 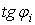 — тангенс кута нахилу дотичної до осі арки в точці
— тангенс кута нахилу дотичної до осі арки в точці  що дозволяє послідовно обчислити значення
що дозволяє послідовно обчислити значення 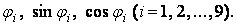
Наприклад,
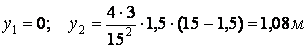 і т.д.
і т.д.
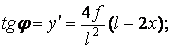
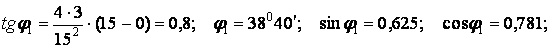
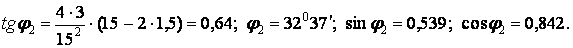
Аналогічні обчислення проведемо для перетинів, що залишилися, 3 – 9. Отримані результати зручно представляти в табличній формі (табл.4.1).
Таблиця 4.1
Визначення ординат епюр у табличній формі
№ 
| х, м | у, м | 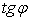
| 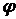
| 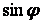
| 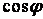
| 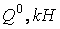
| 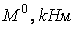
| 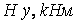
|
| 0,8 | 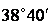
| 0,625 | 0,781 | ||||||
| 1,5 | 1,08 | 0,64 | 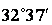
| 0,539 | 0,842 | 70,2 | |||
| 1,92 | 0,48 | 
| 0,433 | 0,902 | 124,8 | ||||
| 2,35 | 0,37 | 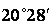
| 0,350 | 0,937 | 152,8 | ||||
| 2,67 | 0,27 | 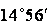
| 0,258 | 0,966 | 173,6 | ||||
| -2 | |||||||||
| 7,5 | -2 | ||||||||
| 2,88 | -0,16 | 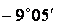
| -0,158 | 0,987 | -2 | 187,2 | |||
| 1,92 | -0,48 | 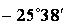
| -0,433 | 0,902 | -32 | 124,8 | |||
| -0,8 | 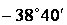
| -0,625 | 0,781 | -62 |
Для визначення балкових зусиль 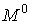 і
і  будуємо епюри згинальних моментів і поперечних сил від заданих навантажень, прикладених до шарнірної балки (мал.4.17, а, б, в).
будуємо епюри згинальних моментів і поперечних сил від заданих навантажень, прикладених до шарнірної балки (мал.4.17, а, б, в).
| а б в | 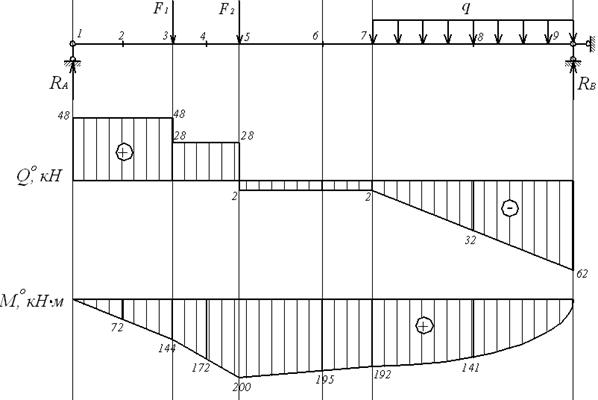
|
Рис.4.17. Визначення балкових зусиль
Ординати цих епюр, що відповідають перетинам 1 – 9, також вносимо в табл.4.1. Для перетинів 3 і 5, у яких прикладені зосереджені сили, визначаємо два значення  — ліворуч і праворуч від кожної із сил.
— ліворуч і праворуч від кожної із сил.
Тепер скористаємося формулами (4.12) – (4.14). Обчислимо спочатку компоненти цих формул, а потім — величини 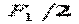 в перетинах 1 – 9. Ця процедура зводиться до арифметичних дій над числами з табл.4.1.
в перетинах 1 – 9. Ця процедура зводиться до арифметичних дій над числами з табл.4.1.
Результати обчислень зведені в табл. 4.2, а отримані епюри 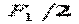 представлені на мал.4.18, а, б, в.
представлені на мал.4.18, а, б, в.
Таблиця 4.2
Обчислення значень 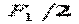 у характерних перетинах
у характерних перетинах
| № | 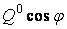
| 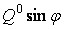
| 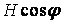
| 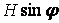
| 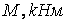
| 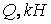
| 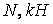
| |
| 37,5 | 50,8 | 40,6 | -3,1 | -80,8 | ||||
| 40,4 | 25,9 | 54,7 | 1,8 | 5,4 | -80,6 | |||
| 43,3 | 20,8 | 58,6 | 28,1 | 19,2 | 15,2 | -79,4 | ||
| 25,3 | 12,1 | -2,8 | -70,7 | |||||
| 26,2 | 9,8 | 60,9 | 22,8 | 19,2 | 3,4 | -70,7 | ||
| 27,0 | 7,2 | 62,8 | 16,8 | 26,4 | 10,2 | -70 | ||
| -1,9 | -0,5 | -18,7 | -62,3 | |||||
| -2 | -2 | -65 | ||||||
| -2 | 0,3 | 64,2 | -10,3 | 4,8 | 8,3 | -64,5 | ||
| -28,9 | 13,9 | 58,6 | -28,1 | 16,2 | -0,8 | -72,5 | ||
| -48,4 | 38,8 | 50,8 | -40,6 | -1,8 | -89,6 | |||
Відзначимо, що всі три епюри є криволінійними. Значення моментів у середині кожної ділянки визначаються по формулі
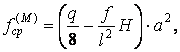
тому що при дії на арку зосереджених сил і рівномірно розподілених навантажень згинальний момент на кожній ділянці змінюється за законом квадратної параболи.
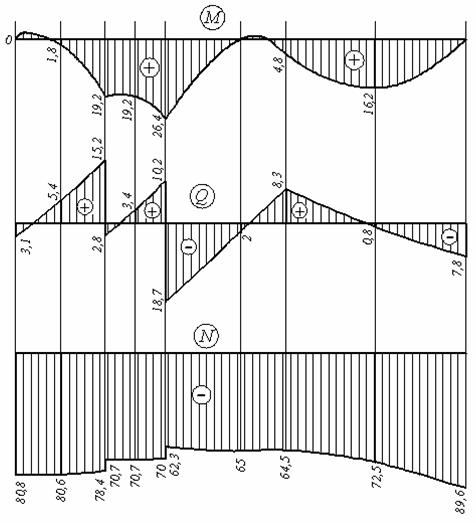
Рис.4.18. Епюри 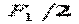
Дата добавления: 2015-01-29; просмотров: 960;
