Точки разрыва функции.
Точка х0 называется точкой разрыва функции ¦(х), если эта функция не является непрерывной. Различают точки разрыва: первого рода (когда существуют конечные односторонние пределы функции слева или справа при х ® х0, не равные друг другу) и второго рода (когда хотя бы один из односторонних пределов слева или справа равен бесконечности или не существует). К точкам разрыва первого рода относят также точки устранимого разрыва, когда предел функции при х ® х0 существует, но не равен значению функции в этой точке.
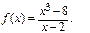 |
Пример 2. Испытать на непрерывность в точке х = 2 функцию
Р е ш е н и е. Так как при х = 2 функция не существует и тем самым нарушено первое условие непрерывности, то в этой точке функция терпит разрыв. Найдем левосторонний и правосторонний пределы функции:
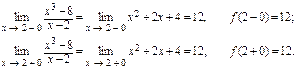 |
Таким образом, существует и предел этой функции при х ® 2, так как ¦(2+0) = ¦(2 - 0). В точке х = 2 разрыв можно «устранить», если значение функции в этой точке принять равным 12, т.е. если условится, что ¦(2) = 2.
Точка х = 2 – точка устранимого разрыва.
Пример 3. Какого рода разрыв имеет функция у = 1/х в точке х = 0.
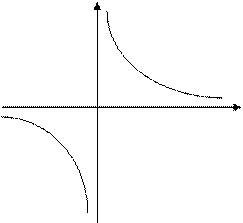 Р е ш е н и е. Левосторонний предел функции в точке х = 0 равен бесконечности со знаком минус, а ее правосторонний предел в точке х = 0 равен бесконечности со знаком плюс. Таким образом, здесь не существует конечного предела ни слева, ни справа, а потому точка х = 0 – точка разрыва второго рода (рис 3).
Р е ш е н и е. Левосторонний предел функции в точке х = 0 равен бесконечности со знаком минус, а ее правосторонний предел в точке х = 0 равен бесконечности со знаком плюс. Таким образом, здесь не существует конечного предела ни слева, ни справа, а потому точка х = 0 – точка разрыва второго рода (рис 3).
у
у = 1/х
0 x
Рис 3.
Дата добавления: 2014-12-16; просмотров: 1071;
