Асимптоты графика функции. Если при неограниченном увеличении модуля аргумента (функции), график функции неограниченно близко приближается к некоторой прямой

Если при неограниченном увеличении модуля аргумента (функции), график функции неограниченно близко приближается к некоторой прямой, то данная прямая называется асимптотой.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Определение 1.6.4. Прямая 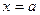называется вертикальной асимптотой графика функции 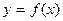, если предел .

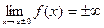Вертикальная асимптота существует в точках разрыва функции либо на границе области определения функции.

Определение 1.6.5. Прямая 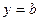называется горизонтальной асимптотой графика функции 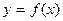, если .

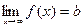Определение 1.6.6. Прямая 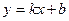называется наклонной асимптотой графика функции 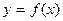, если существуют следующие пределы:

.

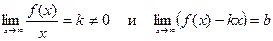Пример 3.Найти асимптоты графика функции .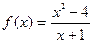

Решение: Найдем вертикальную асимптоту. Точка 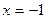является точкой разрыва, причем 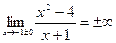. Следовательно, прямая 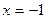является вертикальной асимптотой.

Горизонтальных асимптот нет, так как .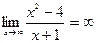

Наклонные асимптоты:

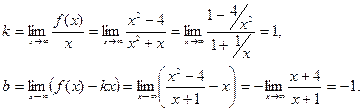
Таким образом, получаем уравнение наклонной асимптоты: .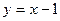

Пример 4.Исследовать функцию и построить график .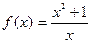

Решение:

1. Область определения функции: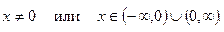

2. Функция является нечетной, так как 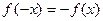. Ее график симметричен относительно начала координат, поэтому достаточно провести исследование на интервале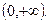

3. Пересечений графика с осями координат нет.

4. Так как 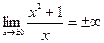, то имеется вертикальная асимптота – ось 0х.

Определим наклонную асимптоту:

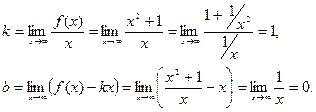
Уравнение наклонной асимптоты: y=x.

5. 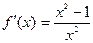, то есть производная обращается в ноль в точках .

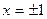Точка 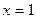- локальный минимум; а точка 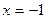- локальный максимум. Значения функции в этих точках соответственно равны: .

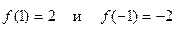Данная функция возрастает на интервалах 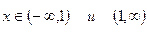; убывает на интервалах .

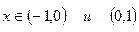6. 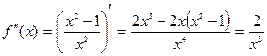. Видно, что вторая производная не обращается в ноль, следовательно, точек перегиба нет.

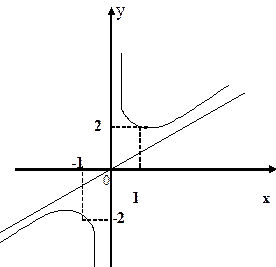
7. График функции имеет вид: