Выпуклость и точки перегиба графика функции.

Определение 1.6.2. Будем говорить, что график функции 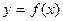на интервале (a, b) выпукл вниз (вверх), если он расположен выше (ниже) любой касательной к графику функции на (a, b).

Способ определения направления выпуклости сформулируем в следующей теореме:

Теорема 1.6.3. Если функция 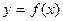имеет на интервале (a, b) вторую производную и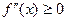 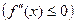на (a, b), то график функции имеет на (a, b) выпуклость, направленную вниз (вверх).

Определение 1.6.3. Точка 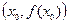называется точкой перегиба графика функции 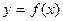, если в ней график имеет касательную и существует такая окрестность точки 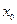, в пределах которой график 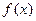имеет разные направления выпуклости.

Сформулируем необходимое и достаточное условия точки перегиба.

Теорема 1.6.4 (необходимое условие).

Пусть график функции 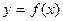имеет перегиб в точке 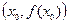и функция 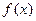имеет в точке 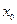непрерывную вторую производную. Тогда .

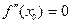Теорема 1.6.5 (достаточное условие).

Пусть функция 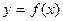имеет вторую производную в некоторой окрестности точки 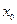, которая имеет разные знаки слева и справа от 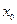. Тогда график 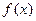имеет перегиб в точке .

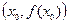Пример 2.Найти интервалы выпуклости и точки перегиба графика функции .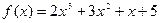

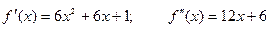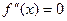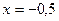Решение: Находим производные: , при . Знаки второй производной:

Функция выпукла вверх на интервале 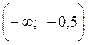и выпукла вниз на интервале 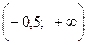; 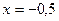- точка перегиба функции.