Точки локального экстремума.
Определение 1.6.1. Точка 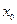 называется точкой локального максимума (минимума) функции
называется точкой локального максимума (минимума) функции 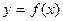 , если для любого
, если для любого 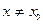 в некоторой окрестности точки
в некоторой окрестности точки 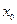 выполнено неравенство
выполнено неравенство
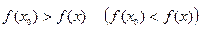 .
.
Локальный минимум и максимум объединены общим названием – локальный экстремум.
Теорема 1.6.1 (необходимое условие локального экстремума).
Если функция 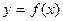 дифференцируема в точке
дифференцируема в точке 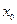 и имеет в этой точке локальный экстремум, то
и имеет в этой точке локальный экстремум, то 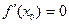 .
.
Геометрически это означает, что если в точках локального экстремума существуют касательные, то они параллельны оси абсцисс.
Теорема 1.6.2 (достаточное условие существование локального экстремума).
Пусть функция 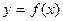 дифференцируема в некоторой окрестности точки
дифференцируема в некоторой окрестности точки 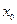 . Если при переходе через точку
. Если при переходе через точку 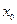 слева направо производная
слева направо производная 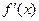 меняет знак с плюса на минус (с минуса на плюс), то в точке
меняет знак с плюса на минус (с минуса на плюс), то в точке 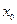 функция
функция 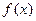 имеет локальный максимум (минимум); в противном случае функция не имеет локального экстремума в точке
имеет локальный максимум (минимум); в противном случае функция не имеет локального экстремума в точке 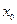 .
.
Пример 1.Найти точки локального экстремума и интервалы монотонности функции 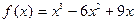 .
.
Решение: Найдем производную 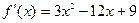 . Приравниваем ее к нулю и решаем уравнение
. Приравниваем ее к нулю и решаем уравнение 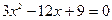 , находим две точки возможного экстремума:
, находим две точки возможного экстремума: 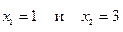 . Видно, что
. Видно, что 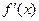 при переходе через точку
при переходе через точку 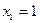
меняет знак с «+» на «-», следовательно, в этой точке локальный максимум; аналогично устанавливается, что в точке 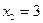 функция имеет локальный минимум.
функция имеет локальный минимум.
Найдем теперь интервалы монотонности функции. Поскольку 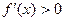 при
при 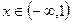 , то функция монотонно возрастает на этом интервале; (1, 3) является интервалом монотонного убывания
, то функция монотонно возрастает на этом интервале; (1, 3) является интервалом монотонного убывания 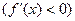 , а на интервале
, а на интервале 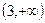 функция снова монотонно возрастает
функция снова монотонно возрастает 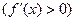 .
.
Дата добавления: 2014-12-04; просмотров: 1114;
