Геометрический смысл.
Пусть 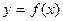 - дифференцируемая функция, тогда
- дифференцируемая функция, тогда 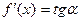 угловой коэффициент касательной, проведенной к данной кривой в некоторой точке.
угловой коэффициент касательной, проведенной к данной кривой в некоторой точке.
Уравнение касательной к кривой 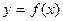 в точке
в точке 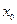 имеет вид:
имеет вид:
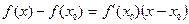
Уравнение нормали в точке 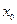 имеет вид:
имеет вид:
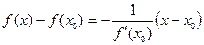
Пример 5.Составить уравнения касательной и нормали к графику функции  в точке с абсциссой
в точке с абсциссой 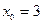 .
.
Решение: Найдем значение функции в точке 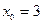 :
: 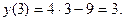
Производная функции: 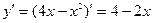 , тогда значение производной в точке
, тогда значение производной в точке 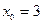 равно:
равно: 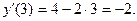
Таким образом, уравнение касательной запишется в виде:
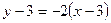 , или
, или 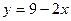 .
.
Уравнение нормали:  , или
, или 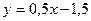 .
.
Дата добавления: 2014-12-04; просмотров: 805;
