Правила дифференцирования.
Пусть 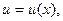
 - дифференцируемые функции в точке x. Тогда справедливы следующие формулы:
- дифференцируемые функции в точке x. Тогда справедливы следующие формулы:
1. 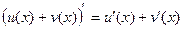 ;
;
2.  ;
;
3. 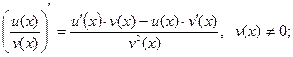
4. Если функция 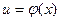 дифференцируема в точке
дифференцируема в точке 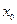 , а функция
, а функция  дифференцируема в точке
дифференцируема в точке 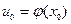 , то сложная функция
, то сложная функция  дифференцируема в точке
дифференцируема в точке 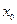 :
:

5. Если 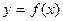 - дифференцируема и строго монотонна на промежутке Х, то функция, обратная к данной
- дифференцируема и строго монотонна на промежутке Х, то функция, обратная к данной 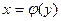 , также дифференцируема и ее производная определяется соотношением:
, также дифференцируема и ее производная определяется соотношением:
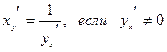
Дата добавления: 2014-12-04; просмотров: 890;
