СРАВНЕНИЕ БЕСКОНЕЧНО МАЛЫХ
Определение 1.4.1. Функция 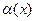 называется бесконечно малой при
называется бесконечно малой при 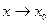 (или в точке
(или в точке 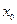 ), если предел ее в этой точке равен нулю, то есть
), если предел ее в этой точке равен нулю, то есть 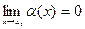 .
.
Справедливо следующее утверждение:
Алгебраическая сумма и произведение конечного числа бесконечно малых функций в точке 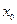 , как и произведение бесконечно малой и ограниченной функций, являются бесконечно малыми функциями в точке
, как и произведение бесконечно малой и ограниченной функций, являются бесконечно малыми функциями в точке 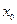 .
.
При вычислении пределов ряда функций полезно использовать замену бесконечно малой функции на эквивалентную ей.
Определение 1.4.2. Пусть 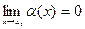 и
и 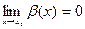 , а
, а 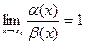 . Тогда a(х) и b(х) называются эквивалентными бесконечно малыми функциями (обозначается a(х) ~ b(х)).
. Тогда a(х) и b(х) называются эквивалентными бесконечно малыми функциями (обозначается a(х) ~ b(х)).
Таблица основных эквивалентных бесконечно малых функций при х® 0:
sin x ~ x arcsin x ~ x
tg x ~ x arctg x ~ x
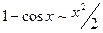 (1+x)a –1 ~ ax
(1+x)a –1 ~ ax
ex – 1 ~ x ln (1+x) ~ x
Пример 1.Вычислить предел 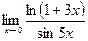 .
.
Решение: Имеем 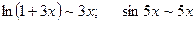 .
.
Поэтому: 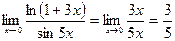
Заметим, что, если у нас есть сумма или разность бесконечно малых функций, то для применения этого правила иногда можно преобразовать данные выражения в произведение.
Пример 2.Вычислить предел 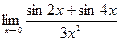 .
.
Решение: 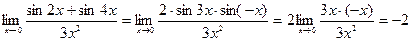 .
.
Дата добавления: 2014-12-04; просмотров: 1066;
