Бесконечное множество решений системы коротко записывают в виде так называемогообщего решения системы.
Общее решение системы найдем с помощью обратного хода метода Гаусса.
Сначала нужно определить, какие переменные у нас являются базисными, а какие переменные свободными. Не обязательно заморачиваться терминами линейной алгебры, достаточно запомнить, что вот существуют такие базисные переменные и свободные переменные.
Базисные переменные всегда «сидят» строго на ступеньках матрицы.
В данном примере базисными переменными являются 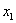 и
и 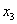
Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: 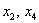 – свободные переменные.
– свободные переменные.
Теперь нужно все базисные переменные выразить только через свободные переменные.
Обратный ход алгоритма Гаусса традиционно работает снизу вверх.
Из второго уравнения системы выражаем базисную переменную 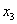 :
:
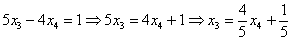
Теперь смотрим на первое уравнение: 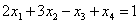 . Сначала в него подставляем найденное выражение
. Сначала в него подставляем найденное выражение 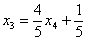 :
:
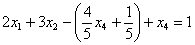
Осталось выразить базисную переменную 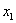 через свободные переменные
через свободные переменные 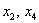 :
:
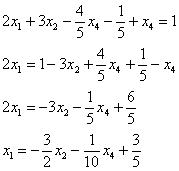
В итоге получилось то, что нужно – все базисные переменные ( 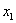 и
и 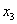 ) выражены только через свободные переменные
) выражены только через свободные переменные 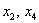 :
:
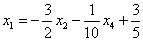
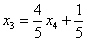
Собственно, общее решение готово:
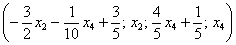
Как правильно записать общее решение?
Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные 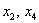 следует записать на второй и четвертой позиции:
следует записать на второй и четвертой позиции:
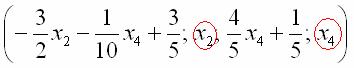 .
.
Полученные же выражения для базисных переменных 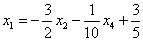 и
и 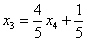 , очевидно, нужно записать на первой и третьей позиции:
, очевидно, нужно записать на первой и третьей позиции:
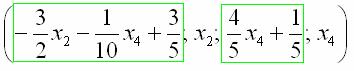
Из общего решения системы можно найти бесконечно много частных решений. Это очень просто.
Свободным переменным 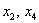 можно придавать любые значения. Самыми популярными значениями являются нулевые значения, поскольку частное решение получается проще всего. Подставим
можно придавать любые значения. Самыми популярными значениями являются нулевые значения, поскольку частное решение получается проще всего. Подставим 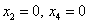 в общее решение:
в общее решение:
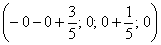
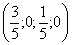 – частное решение.
– частное решение.
Другой сладкой парочкой являются единицы, подставим 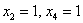 в общее решение:
в общее решение:
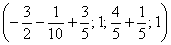
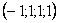 – еще одно частное решение.
– еще одно частное решение.
Легко заметить, что система уравнений имеет бесконечно много решений (так как свободным переменным мы можем придать любые значения)
Каждое частное решение должно удовлетворять каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение 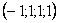 и подставьте его в левую часть каждого уравнения исходной системы:
и подставьте его в левую часть каждого уравнения исходной системы:
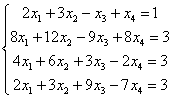
Всё должно сойтись. И с любым полученным вами частным решением – тоже всё должно сойтись.
Но, строго говоря, проверка частного решения иногда обманывает, т.е. какое-нибудь частное решение может удовлетворять каждому уравнению системы, а само общее решение на самом деле найдено неверно.
Поэтому более основательна и надёжна проверка общего решения. Как проверить полученное общее решение 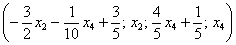 ?
?
Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае 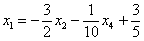 и
и 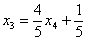 , и подставить их в левую часть каждого уравнения системы.
, и подставить их в левую часть каждого уравнения системы.
В левую часть первого уравнения системы:
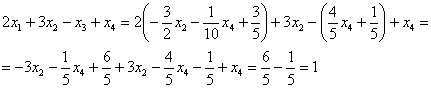
Получена правая часть исходного уравнения.
В левую часть второго уравнения системы:
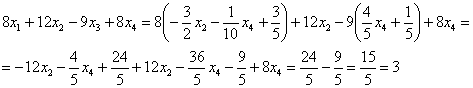
Получена правая часть исходного уравнения.
И далее – в левые части третьего и четвертого уравнение системы. Это дольше, но зато гарантирует стопроцентную правильность общего решения. Кроме того, в некоторых заданиях требуют проверку общего решения.
Пример 4
Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения.
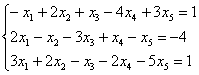
Это пример для самостоятельного решения. Здесь, кстати, снова количество уравнений меньше, чем количество неизвестных, а значит, сразу понятно, что система будет либо несовместной, либо с бесконечным множеством решений. Что важно в самом процессе решения? Внимание, и еще раз внимание. Полное решение и ответ в конце урока.
И еще пара примеров для закрепления материала
Пример 5
Решить систему линейных уравнений. Если система имеет бесконечно много решений, найти два частных решения и сделать проверку общего решения
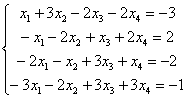
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
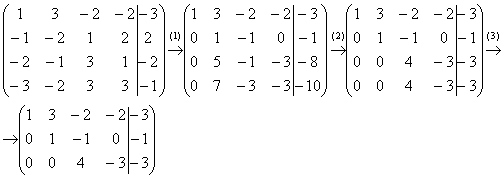
(1) Ко второй строке прибавляем первую строку. К третьей строке прибавляем первую строку, умноженную на 2. К четвертой строке прибавляем первую строку, умноженную на 3.
(2) К третьей строке прибавляем вторую строку, умноженную на –5. К четвертой строке прибавляем вторую строку, умноженную на –7.
(3) Третья и четвертая строки одинаковы, одну из них удаляем.
Вот такая красота:
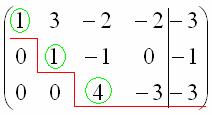
Базисные переменные сидят на ступеньках, поэтому 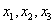 – базисные переменные.
– базисные переменные.
Свободная переменная, которой не досталось ступеньки здесь всего одна: 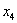
Обратный ход:
Выразим базисные переменные через свободную переменную:
Из третьего уравнения:
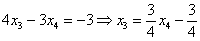
Рассмотрим второе уравнение 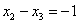 и подставим в него найденное выражение
и подставим в него найденное выражение 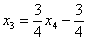 :
:
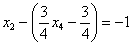
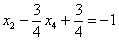
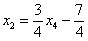
Рассмотрим первое уравнение 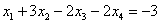 и подставим в него найденные выражения
и подставим в него найденные выражения 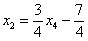 и
и 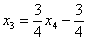 :
:
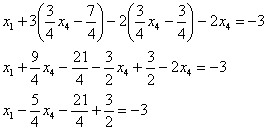
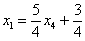
Да, всё-таки удобен калькулятор, который считает обыкновенные дроби.
Таким образом, общее решение:
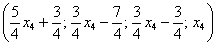
Еще раз, как оно получилось? Свободная переменная 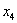 одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных
одиноко сидит на своём законном четвертом месте. Полученные выражения для базисных переменных 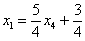 ,
, 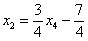 ,
, 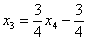 тоже заняли свои порядковые места.
тоже заняли свои порядковые места.
Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =)
Подставляем трех богатырей 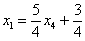 ,
, 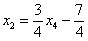 ,
, 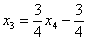 в левую часть каждого уравнения системы:
в левую часть каждого уравнения системы:
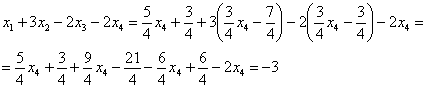
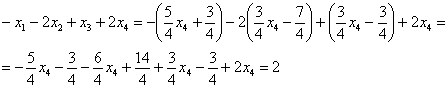
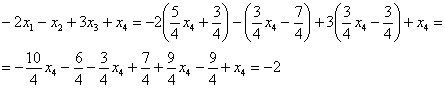
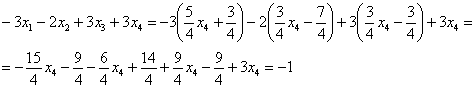
Получены соответствующие правые части уравнений, таким образом, общее решение найдено верно.
Теперь из найденного общего решения 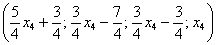 получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная
получим два частных решения. Шеф-поваром здесь выступает единственная свободная переменная 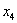 . Ломать голову не нужно.
. Ломать голову не нужно.
Пусть 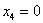 , тогда
, тогда 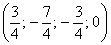 – частное решение.
– частное решение.
Пусть 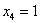 , тогда
, тогда 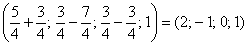 – еще одно частное решение.
– еще одно частное решение.
Ответ: Общее решение: 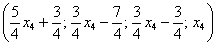 , частные решения:
, частные решения: 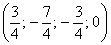 ,
, 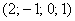 .
.
Зря я тут вспомнил про негров, потому-что в голову полезли всякие садистские мотивы, и вспомнилась карикатура, где куклуксклановцы в своих белых балахонах бегут по футбольному полю за чернокожим футболистом. Сижу, тихо улыбаюсь. Знаете, как отвлекает….
Много математики вредно, поэтому похожий заключительный пример для самостоятельного решения.
Пример 6
Найти общее решение системы линейных уравнений.
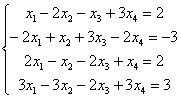
Проверка общего решения у меня уже сделана, ответу можно доверять. Ваш ход решения может отличаться от моего хода решения, главное, чтобы совпали общие решения.
Наверное, многие заметили неприятный момент в решениях: очень часто при обратном ходе метода Гаусса нам пришлось возиться с обыкновенными дробями. На практике это действительно так, случаи, когда дробей нет – встречаются значительно реже. Будьте готовы морально, и, самое главное, технически.
Остановлюсь на некоторых особенностях решения, которые не встретились в прорешанных примерах.
В общее решение системы иногда может входить константа (или константы), например: 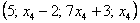 . Здесь одна из базисных переменных равна постоянному числу:
. Здесь одна из базисных переменных равна постоянному числу: 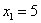 . В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.
. В этом нет ничего экзотического, так бывает. Очевидно, что в данном случае любое частное решение будет содержать пятерку на первой позиции.
Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и, как ни странно, может иметь единственное решение.
И, конечно, повторюсь в своем совете – чтобы комфортно себя чувствовать при решении системы методом Гаусса, следует набить руку и прорешать хотя бы десяток систем.
Желаю успехов!
Решения и ответы:
Пример 2: Решение:Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
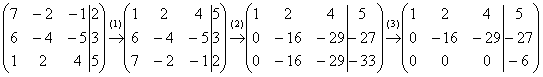
Выполненные элементарные преобразования:
(1) Первую и третью строки поменяли местами.
(2) Ко второй строке прибавили первую строку, умноженную на –6. К третьей строке прибавили первую строку, умноженную на –7.
(3) К третьей строке прибавили вторую строку, умноженную на –1.
В результате элементарных преобразований получена строка вида 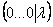 , где
, где 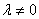 , значит, система несовместна.
, значит, система несовместна.
Ответ: решений нет.
Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
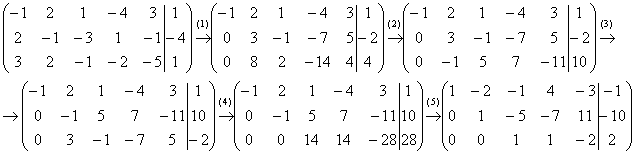
Выполненные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на 2. К третьей строке прибавили первую строку, умноженную на 3.
Для второй ступеньке нет единицы, и преобразование (2) направлено на её получение.
(2) К третьей строке прибавили вторую строку, умноженную на –3.
(3) Вторую с третью строки поменяли местами (переставили полученную –1 на вторую ступеньку)
(4) К третьей строке прибавили вторую строку, умноженную на 3.
(5)У первых двух строк сменили знак (умножили на –1), третью строку разделили на 14.
Обратный ход.
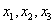 – базисные переменные (те, которые на ступеньках),
– базисные переменные (те, которые на ступеньках), 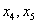 – свободные переменные (те, кому не досталось ступеньки).
– свободные переменные (те, кому не досталось ступеньки).
Выразим базисные переменные через свободные переменные:
Из третьего уравнения: 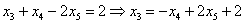
Рассмотрим второе уравнение: 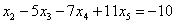
Подставим в него найденное выражение 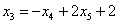 :
:
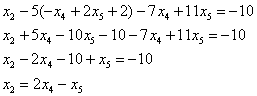
Рассмотрим первое уравнение: 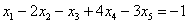
Подставим в него найденные выражения: 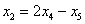 ,
, 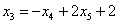 :
:
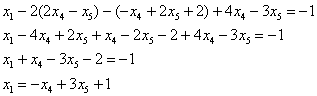
Общее решение: 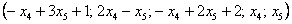
Найдем два частных решения
Если 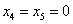 , то
, то 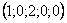
Если 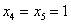 , то
, то 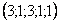
Ответ:Общее решение: 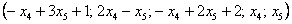 , частные решения:
, частные решения: 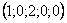 ,
, 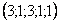 .
.
Проверка: подставим найденное решение (выражения базисных переменных 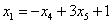 ,
, 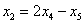 и
и 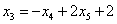 ) в левую часть каждого уравнения системы:
) в левую часть каждого уравнения системы:
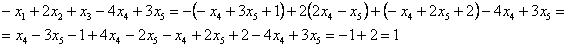
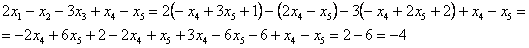
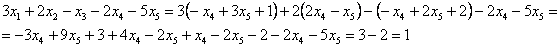
Получены соответствующие правые части, таким образом, общее решение найдено верно.
Пример 6: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
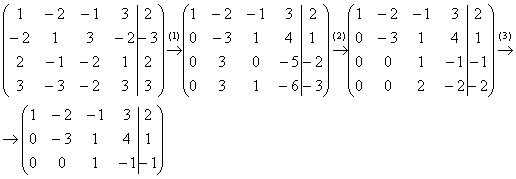
(1) Ко второй строке прибавляем первую строку, умноженную на 2. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –3.
(2) К третьей строке прибавляем вторую строку. К четвертой строке прибавляем вторую строку.
(3) Третья и четвертая строки пропорциональны, одну из них удаляем.
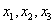 – базисные переменные,
– базисные переменные, 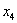 – свободная переменная. Выразим базисные переменные через свободную переменную:
– свободная переменная. Выразим базисные переменные через свободную переменную:
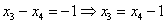
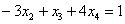
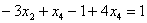
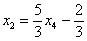
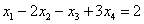
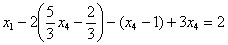
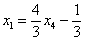
Ответ: Общее решение: 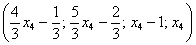
Дата добавления: 2014-11-29; просмотров: 4337;
