Несовместные системы. Системы с общим решением. Частные решения
Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом, методом Гаусса. Однако на практике широко распространены еще два случая:
– Система несовместна (не имеет решений);
– Система имеет бесконечно много решений.
Для этих систем применяют наиболее универсальный из всех способов решения – метод Гаусса. На самом деле, к ответу приведет и «школьный» способ, но в высшей математике принято использовать гауссовский метод последовательного исключения неизвестных. Те, кто не знаком с алгоритмом метода Гаусса, пожалуйста, сначала изучите урок метод Гаусса для чайников.
Сами элементарные преобразования матрицы – точно такие же, разница будет в концовке решения. Сначала рассмотрим пару примеров, когда система не имеет решений (несовместна).
Пример 1
Решить систему линейных уравнений
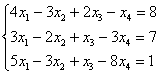
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить.
Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
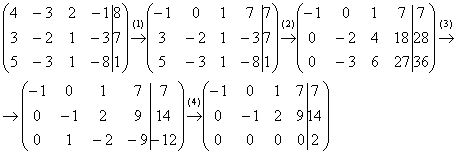
(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.
(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.
(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.
(4) К третьей строке прибавляем вторую строку.
Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: 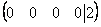 . Ясно, что так быть не может. Действительно, перепишем полученную матрицу
. Ясно, что так быть не может. Действительно, перепишем полученную матрицу  обратно в систему линейных уравнений:
обратно в систему линейных уравнений: 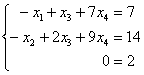
Дата добавления: 2014-11-29; просмотров: 3396;
