Если в результате элементарных преобразований получена строка вида , где – число, отличное от нуля, то система несовместна (не имеет решений).

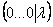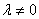Как записать концовку задания? Необходимо записать фразу «в результате элементарных преобразований получена строка вида , где » и дать ответ: система не имеет решений (несовместна).

Обратите внимание, что нет никакого обратного хода алгоритма Гаусса, решений нет и находить попросту нечего.

Пример 2

Решить систему линейных уравнений

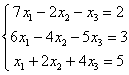
Это пример для самостоятельного решения. Полное решение и ответ в конце урока. Снова напоминаю, что ваш ход решения может отличаться от моего хода решения, у алгоритма Гаусса нет сильной «жёсткости».

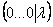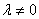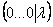Еще одна техническая особенность решения: элементарные преобразования можно прекращать сразу же, как только появилась строка вида , где . Рассмотрим условный пример: предположим, что после первого же преобразования получилась матрица . Матрица еще не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет никакой необходимости, так как появилась строка вида , где 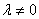. Следует сразу дать ответ, что система несовместна.

Когда система линейных уравнений не имеет решений – это почти подарок, ввиду того, что получается короткое решение, иногда буквально в 2-3 действия.

Но всё в этом мире уравновешено, и задача, в которой система имеет бесконечно много решений – как раз длиннее.

Пример 3

Решить систему линейных уравнений

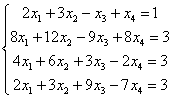
Тут 4 уравнений и 4 неизвестных, таким образом, система может иметь либо единственное решение, либо не иметь решений, либо иметь бесконечно много решений. Как бы там ни было, но метод Гаусса в любом случае приведет нас к ответу. В этом его и универсальность.

Начало опять стандартное. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

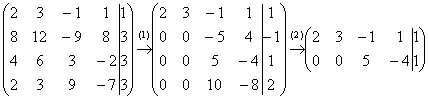
Вот и всё, а вы боялись.

(1) Обратите внимание, что все числа в первом столбце делятся на 2, поэтому на левой верхней ступеньке нас устраивает и двойка. Ко второй строке прибавляем первую строку, умноженную на –4. К третьей строке прибавляем первую строку, умноженную на –2. К четвертой строке прибавляем первую строку, умноженную на –1.

Внимание! У многих может возникнуть соблазн из четвертой строки вычесть первую строку. Так делать можно, но не нужно, опыт показывает, что вероятность ошибки в вычислениях увеличивается в несколько раз. Только складываем: К четвертой строке прибавляем первую строку, умноженную на –1 – именно так!

(2) Последние три строки пропорциональны, две из них можно удалить.

Здесь опять нужно проявить повышенное внимание, а действительно ли строки пропорциональны? Для перестраховки (особенно, чайнику) не лишним будет вторую строку умножить на –1, а четвертую строку разделить на 2, получив в результате три одинаковые строки. И только после этого удалить две из них.

В результате элементарных преобразований расширенная матрица системы приведена к ступенчатому виду:

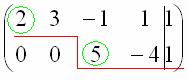
При оформлении задачи в тетради желательно для наглядности делать такие же пометки карандашом.

Перепишем соответствующую систему уравнений:

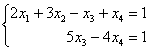
«Обычным» единственным решением системы здесь и не пахнет. Нехорошей строки 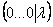тоже нет. Значит, это третий оставшийся случай – система имеет бесконечно много решений.