Cписок производных простейших элементарных функций

1.

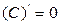
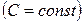
2. 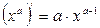, а – любое число

3. 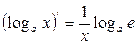, в частности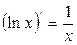

4. 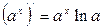, в частности, при :

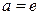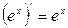
5.

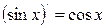
6.

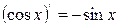
7.

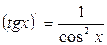
8.

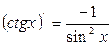
9.

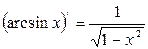
10.

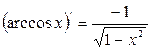
11.

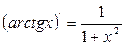
12.

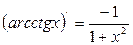
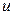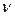Если функции и дифференцируемы в точке х, то:

- Их сумма дифференцируема в точке х и 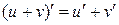(теорема о дифференцировании суммы);

- Произведение функци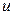й и 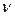дифференцируемо в точке х и 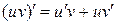(теорема о дифференцировании произведения);

- Частное функци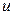й и 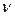дифференцируемо в точке х, есл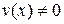и , и 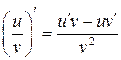(теорема о дифференцировании частного).