Первообразная и интеграл
Пусть на интервале (а, b) задана непрерывная функция f(х). По определению функция F(х) называется первообразной функцией для f(х) на интервале (а, b), если на нем производная от F(х) равна f(х):
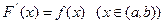
Очевидно, что если функция 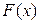 - первообразная для f(х) на (а,b), а С – некоторая постоянная, то функция
- первообразная для f(х) на (а,b), а С – некоторая постоянная, то функция 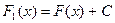 есть также первообразная для f(х), потому, что
есть также первообразная для f(х), потому, что
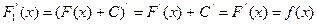
Если F(х) какая-либо первообразная от f(х) на интервале (а, b), то возможные первообразные от f(х) на этом интервале выражаются формулой 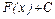 , где вместо С можно подставить любое число.
, где вместо С можно подставить любое число.
Неопределенным интегралом от непрерывной функции f(х) на интервале (а, b) называется произвольная ее первообразная функция. Неопределенный интеграл обозначается так:
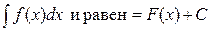 .
.
Если 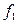 ,
, 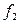 – непрерывные на интервале (а, b) функции и
– непрерывные на интервале (а, b) функции и 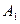 , и
, и 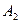 – постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
– постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
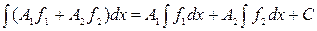 ,
,
где С – некоторая постоянная.
Список основных неопределенных интегралов
1. 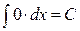 ;
;
2. 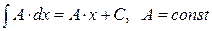 ;
;
3. 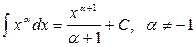 ;
;
4. 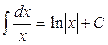 ;
;
5. 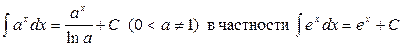 ;
;
6. 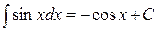 ;
;
7. 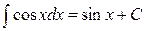 ;
;
8. 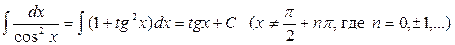
9. 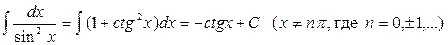
10. 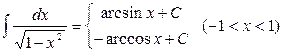 ;
;
11. 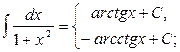
12. 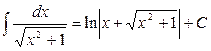 ;
;
13. 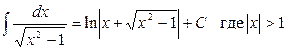 ;
;
14. 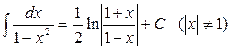
Дата добавления: 2014-12-05; просмотров: 1264;
