Всегда ли существует несобственный интеграл ?
Нет, не всегда.
Подынтегральная функция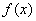
должна быть непрерывной на интервале
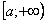.Строго говоря, последнее утверждение неверно: если есть разрывы функции, то в ряде случаев можно разбить интервал на несколько частей и вычислить несколько несобственных интегралов.
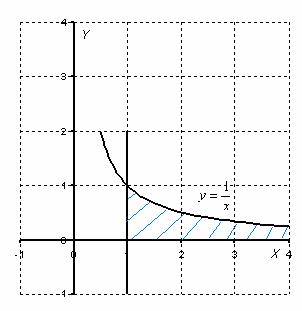
Изобразим на чертеже график подынтегральной функции 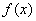. Типовой график и криволинейная трапеция для данного случая выглядит так:
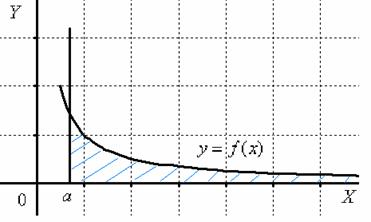
Здесь всё хорошо, подынтегральная функция 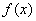непрерывна на интервале 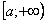, а, значит, несобственный интеграл существует. Обратите внимание, что криволинейная трапеция у нас – бесконечная (не ограниченная справа) фигура.
Несобственный интеграл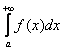
численно равен площади заштрихованной фигуры, при этом возможны два случая:
1) Первая мысль, которая приходит в голову: «Раз фигура бесконечная, то и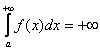 
», иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что, что несобственный интеграл расходится.
2) Но! Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например:
.
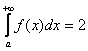Может ли так быть? Да. В этом случае несобственный интеграл сходится.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции .
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл
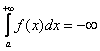
«расходится», либо равен отрицательному числу.
Несобственный интеграл может быть отрицательным.
Важно!Когда Вам для решения предложен ПРОИЗВОЛЬНЫЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно. Ваша задача найти ЧИСЛО, либо доказать, что несобственный интеграл расходится. Геометрический смысл несобственного интеграла рассказан только для того, чтобы легче было понять материал.
Поскольку несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница:
.
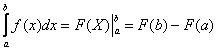На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: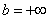 
. Наверное, многие догадались, что здесь необходимо применение теории пределов, и формула запишется так:
.
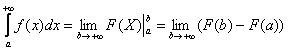В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию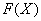 
(неопределенный интеграл) и уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений, ибо лучше поздно, чем в армии. Рассмотрим два классических примера:
Пример 1
Вычислить несобственный интеграл или установить его расходимость.
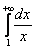
Для наглядности построим чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно.
Подынтегральная функция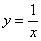 
непрерывна на интервале 
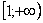, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы
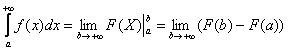
и решение задачи выглядит так:
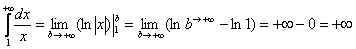
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы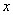 
«динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому-что любая буква ничем не хуже стандартного «икса».
Если Вам непонятно почему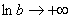 
при 
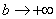, то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций.
Дата добавления: 2014-11-29; просмотров: 2452;