Всегда смотрим и записываем, является ли подынтегральная функция непрерывной на интервале интегрирования.

Пример 2

Вычислить несобственный интеграл или установить его расходимость:
.

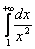Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция

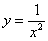
непрерывна на интервале 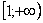. Хорошо. Решаем с помощью формулы

:

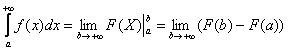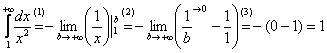
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

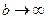(3) Указываем, что , если (это нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на полубесконечном интервале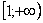

“

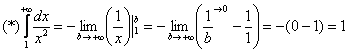
Пример 3

Вычислить несобственный интеграл или установить его расходимость.

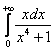
Подынтегральная функция непрерывна на .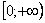

Интеграл не так прост, особенно для чайника. Что делать, если интеграл кажется не самым простым или не сразу понятно как его решать? В этом случае целесообразно применить алгоритм, о котором я уже рассказал в статье Определенный интеграл. Примеры решений.

Сначала попытаемся найти первообразную функцию F(X) (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс:

.

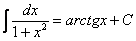Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

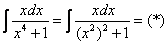
Проведем замену 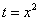, тогда:

.

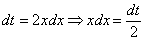
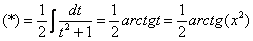Неопределенный интеграл найден, константу C в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

.

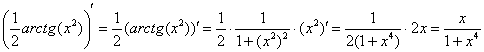Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

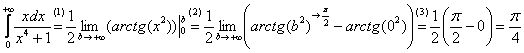
(1) Записываем решение в соответствии с формулой

.

Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница.

Почему 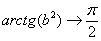при 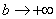? Смотрите график арктангенса.

(3) Получаем окончательный ответ. Тот факт, что arctg(0) = 0, полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

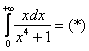
Подынтегральная функция непрерывна на интервале .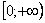

.

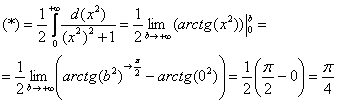А сейчас два примера для самостоятельного решения.

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

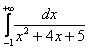
ВНИМАНИЕ!Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

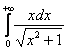
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка. Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения определённых и несобственных интегралов. Там же разобран случай, когда оба предела интегрирования бесконечны.