D) Осы кесіндіде функция шенелген болуы керек
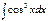 интегралын табыңыз: sinx-sin3x\3+C
интегралын табыңыз: sinx-sin3x\3+C
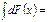 F(x)+C
F(x)+C
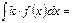
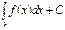
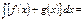
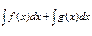
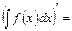 f(x)
f(x)
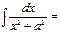 1\a arctgx\a+C
1\a arctgx\a+C
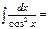 tgx+C
tgx+C
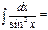 -ctgx+C
-ctgx+C
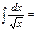 2x+C
2x+C
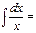 ln[x[+C
ln[x[+C
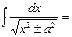 ln[x+√x2+a2[+C
ln[x+√x2+a2[+C
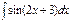 анықталмаған интегралын есептеңіз: -1\2cos(2x+3)+C
анықталмаған интегралын есептеңіз: -1\2cos(2x+3)+C
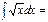 2√x3\3+C
2√x3\3+C
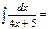 1\4ln[4x+5[+C
1\4ln[4x+5[+C
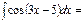 1\3 sin(3x-5)+C
1\3 sin(3x-5)+C
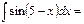 -cos(5-x)
-cos(5-x)
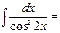 1\2 tg2x+C
1\2 tg2x+C
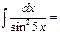 -1\5ctg5x+C
-1\5ctg5x+C
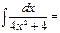 1\4arctgx+C
1\4arctgx+C
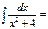 1\2arctgx\2+C
1\2arctgx\2+C
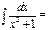 arctgx+C
arctgx+C
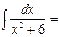 1\2x*ln(x2+6)+C
1\2x*ln(x2+6)+C
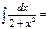 1\2*arctgx\2+C
1\2*arctgx\2+C
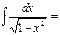 arcsinx+C
arcsinx+C
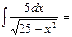 5arcsinx\5+C
5arcsinx\5+C
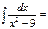 1\6ln[x-3\x+3[+C
1\6ln[x-3\x+3[+C
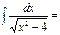 ln[x+√x2-4+C
ln[x+√x2-4+C
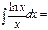 ln2x\2+C
ln2x\2+C
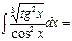 3\5√tg5x+C
3\5√tg5x+C
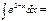 -e2-x+C
-e2-x+C
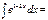 -1\2 e1-2x+C
-1\2 e1-2x+C
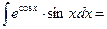 -ecosx+C
-ecosx+C
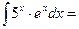 (5e)3\1+ln5+C
(5e)3\1+ln5+C
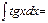 -ln[cosx[+C
-ln[cosx[+C
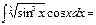 2\5√sin5x+C
2\5√sin5x+C
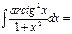 arctg3x\3+C
arctg3x\3+C
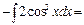 x+sin2x\2+c
x+sin2x\2+c
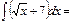 2\3√x3+7x+C
2\3√x3+7x+C
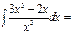 3x+2\x+C
3x+2\x+C
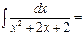 arctg(x+1)+C
arctg(x+1)+C
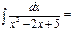 1\2arctg(x-1)\2+C
1\2arctg(x-1)\2+C
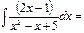 ln[x2-x+5[+C
ln[x2-x+5[+C
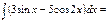 -3cosx-5sin2x\2+C
-3cosx-5sin2x\2+C
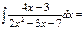 ln[2x2-3x-7[+C
ln[2x2-3x-7[+C
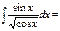 -2√cosx+C
-2√cosx+C
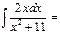 ln[x2+11[+C
ln[x2+11[+C
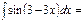 1\3cos(3-3x)+C
1\3cos(3-3x)+C
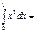 1\4
1\4
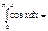 √2\2
√2\2
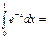 1-e-1
1-e-1
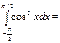 π\2
π\2
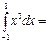 0
0
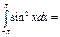 π
π
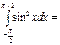 π\2
π\2
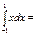 0
0
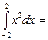 16\3
16\3
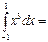 0
0
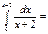 1-ln2
1-ln2
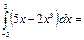 0
0
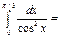 √3
√3
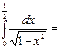 π\6
π\6
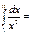 1
1
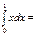 1\2
1\2
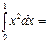 1\3
1\3
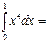 1\5
1\5
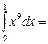 1\10
1\10
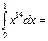 1\15
1\15
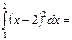 1\3
1\3
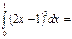 0
0
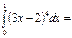 33\15
33\15
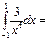 -6\5
-6\5
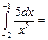 -75\64
-75\64
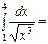 1
1
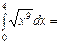 4096\11
4096\11
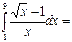 4-ln9
4-ln9
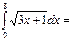 248\9
248\9
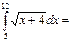 74\3
74\3
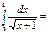 2
2
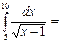 2
2
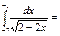 2
2
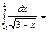 2
2
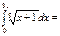 105\2
105\2
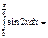 1\4
1\4
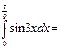 1\6
1\6
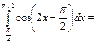 1\2
1\2
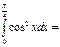 π+2\8
π+2\8
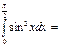 π\4
π\4
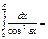 -√3\2
-√3\2
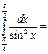 2√3\3
2√3\3
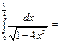 π\4
π\4
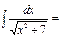 ln|x+√x2+7|+C
ln|x+√x2+7|+C
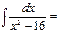 1\8 ln|x-4\x+4|+C
1\8 ln|x-4\x+4|+C
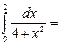 π\8
π\8
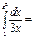 2\3
2\3
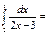 1\2ln5
1\2ln5
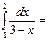 ln2
ln2
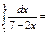 1\2ln3
1\2ln3
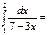 1\3ln4
1\3ln4
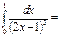 0
0
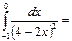 1\24
1\24
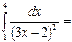 3\10
3\10
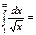 жинақсыз
жинақсыз
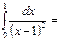 жинақсыз
жинақсыз
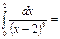 жинақсыз
жинақсыз
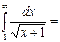 жинақсыз
жинақсыз
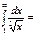 жинақсыз
жинақсыз
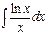 анықталмаған интегралын есептеңіз: ln2x\c+C
анықталмаған интегралын есептеңіз: ln2x\c+C
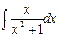 анықталмаған интегралын есептеңіз:1\2ln(x2+1)+C
анықталмаған интегралын есептеңіз:1\2ln(x2+1)+C
А
$$$ 1 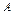 мен
мен 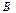 жиындарының бірігуін көрсетіңіз C={x: x
жиындарының бірігуін көрсетіңіз C={x: x 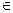 A немесе x
A немесе x 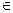 B}
B}
$$$ 2 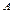 мен
мен 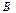 жиындарының қиылысуын көрсетіңіз C={x: x
жиындарының қиылысуын көрсетіңіз C={x: x 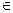 A және x
A және x 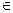 B}
B}
$$$ 3 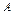 мен
мен 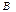 жиындарының айырымын көрсетіңіз C={x: x
жиындарының айырымын көрсетіңіз C={x: x 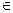 A және x
A және x 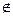 B}
B}
$$$ 8 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} жиындарының бірігуін көрсетіңіз. 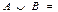
C) {2, -3, 0, а, б, в, -1, 4}
$$$ 9 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} ж-ң қиылысуын көрсетіңіз. 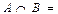 D) {0, в}
D) {0, в}
$$$10 A={2, -3, 0, a, б, в} мен B={-1, 0, 4, в} ж-ң айырымын көрсетіңіз. 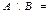 E) {2, -3, а, б}
E) {2, -3, а, б}
$$$ 11 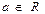 нақты санының e маңайын көрсетіңіз (e >0): A) {x
нақты санының e маңайын көрсетіңіз (e >0): A) {x 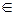 R: a-e < x < a+e}
R: a-e < x < a+e}
$$$ 12 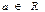 нақты с-ң оң жақ e маңайын көрсетіңіз (e >0): B) {x
нақты с-ң оң жақ e маңайын көрсетіңіз (e >0): B) {x 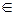 R: a ≤ x < a+e}
R: a ≤ x < a+e}
$$13 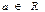 нақты санының сол жақ e маң-н көрсетіңіз (e >0): C) {x
нақты санының сол жақ e маң-н көрсетіңіз (e >0): C) {x 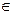 R: a-e < x ≤ a}
R: a-e < x ≤ a}
$$$ 14 a= +∞ (плюс ақырсыздық) нүктесінің e маңайын көрсетіңіз (e >0): D) (e, +∞]
$$$ 15 a= -∞ (минус ақырсыздық) нүктесінің e маңайын көрсетіңіз (e >0): E) [-∞; -e)
$$$ 16 a= ∞ (ақырсыздық) нүктесінің e маңайын көрсетіңіз (e >0): A) [-∞; -e) 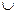 (e; +∞]
(e; +∞]
$$$128 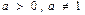 үшін,
үшін, 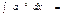
E) 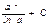
$$$ 208 Айнымалдары ажыратылған бірінші ретті дифференциалдық теңдеуді көрсетіңіз
C) 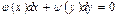
$$$ 209 Айнымалдары ажыратылатын бірінші ретті дифференциалдық теңдеуді көрсетіңіз
D) 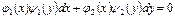
Б
$$$149 Берілген кесіндіде функцияның интегралдануының қажетті шартын көрсетіңіз.
D) Осы кесіндіде функция шенелген болуы керек
$$$170
Бірінші текті меншіксіз интегралдын анықтамасын көрсетіңіз
Е) 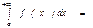
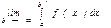
$$$&& Біртекті бірінші ретті дифференциалдық теңдеуді көрсетіңіз E) 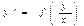
$$$ 213 Бернулли теңдеуін (дифференциалдық) көрсетіңіз
С) 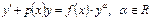
$$$ 214 Біртекті бірінші ретті дифференциалдық теңдеуді айнымалдары ажыратылатын теңдеуге келтіретін айнымал ауыстыруын көрсетіңіз
D) 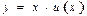
$$$ 216 Бернулли теңдеуін шешуге арналған айнымал ауыстыруын көрсетіңіз A) 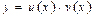
$$$ 217 Бернулли теңдеуін сызықтық теңдеуге келтіретін айнымал ауыстыруын көрсетіңіз
B) 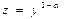
В
$$$169
Винттік сызықтың ұзындығын табыңыз: 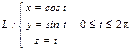 . D)
. D) 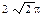
Д
$$$236 Дифференциалдық теңдеудің реті деп:
Дата добавления: 2014-12-02; просмотров: 1933;
