Метод решения определенного интеграла от четной функции по симметричному относительно нуля отрезку

Рассмотрим определенный интеграл вида

.

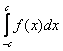Легко заметить, что отрезок интегрирования [-c; c] симметричен относительно нуля.

Если подынтегральная функция 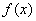является чётной, то интеграл

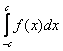
можно вычислить по половине отрезка, а результат – удвоить:

.

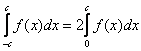Многие догадались, почему так, тем не менее, рассмотрим конкретный пример с чертежом:

Пример 1

Вычислить определенный интеграл

О чётности функции много говорилось в методическом материале Графики и свойства элементарных функций. Повторим один раз: функция является чётной, если для неё выполняется равенство .

Как проверить функцию на чётность? Нужно вместо«икс» подставить .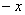

В данном случае: и ,

значит, данная функция является чётной.

Согласно правилу, на симметричном относительно нуля отрезке [-2; 2] наш интеграл от чётной функции можно вычислить следующим образом:

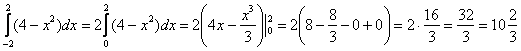
А сейчас геометрическая интерпретация. Да, продолжаем мучить несчастную параболу….

Любая чётная функция, в частности , симметрична относительно оси OY:

Определенный интеграл

численно равен площади плоской фигуры, которая заштрихована зеленым цветом. Но, в силу чётности подынтегральной функции, а, значит, и симметричности её графика относительно оси OY, достаточно вычислить площадь фигуры, заштрихованной синим цветом, а результат – удвоить. Одинаковые же половинки! Именно поэтому справедливо действие

Аналогичная история происходит с любой чётной функцией 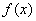по симметричному относительно нуля отрезку:

Некоторые скажут: «Да зачем это всё нужно, можно ведь и так вычислить определенный интеграл». Можно. Давайте вычислим:

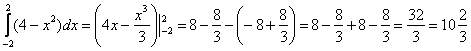
Но удобно ли было подставлять отрицательный нижний предел? Не очень-то. Кстати, ненулевой процент студентов допустит ошибку в знаках. Гораздо проще и приятнее подставить ноль. Замечу, что это еще был простой демонстрационный пример, на практике всё бывает хуже. Кроме того, рассматриваемый прием часто применяется при вычислении двойных интегралов, тройных интегралов, где вычислений и так хватает. Короткий разминочный пример для самостоятельного решения:

Пример 2

Вычислить определенный интеграл

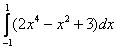
Полное решение и ответ в конце урока.

Обратите внимание, что когда вам предложено просто вычислить определенный интеграл, то чертеж выполнять не нужно! Иллюстрация к Примеру 1 дана только для того, чтобы было понятно правило. Как раз данному моменту посвящена следующая простая задачка:

Пример 3

1) Вычислить определенный интеграл

.

2) Вычислить площадь плоской фигуры, ограниченной линиями

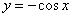, и осью OX на интервале .

Это две разные задачи!Об этом уже говорилось в статье Как вычислить площадь плоской фигуры? Сначала разберемся с первым пунктом:

1) Подынтегральная функция является чётной, отрезок интегрирования симметричен относительно нуля, поэтому:

Определенный интеграл получился отрицательным и так бывает!

3) Теперь найдем площадь плоской фигуры. Вот здесь без чертежа обойтись трудно:

На отрезке график функции расположен ниже оси OX, поэтому:

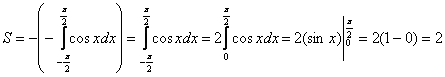
Площадь не может быть отрицательной, именно поэтому в формуле вычисления площади добавляют минус (см. также Пример 3 урока Определенный интеграл. Как вычислить площадь фигуры).

Заметьте, что чётность косинуса никто не отменял, поэтому мы опять споловинили отрезок, и удвоили интеграл.