Метод решения несобственного интеграла с бесконечным нижним пределом

Второй раздел статьи предназначен для тех, кто хорошо разобрался с уроком Несобственные интегралы. Примеры решения, или, по крайне мере, понял бОльшую его часть. Речь пойдет о несобственных интегралах первого рода с бесконечным нижним пределом:

.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

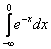
Чем отличается данный интеграл от «обычного» несобственного интеграла с бесконечным верхним пределом? По технике решения практически ничем. Так же нужно найти первообразную (неопределенный интеграл), так же нужно использовать предел при вычислении интеграла. Отличие состоит в том, что необходимо устремить нижний предел интегрирования к «минус бесконечности»:

.

Из вышесказанного следует очевидная формула для вычисления такого несобственного интеграла:

В данном примере, подынтегральная функция непрерывна на и:

,

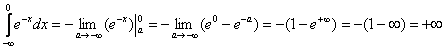то есть, несобственный интеграл расходится.

Вот тут, главное, быть аккуратным в знаках и не забывать, что . Нужно внимательно разобраться, что куда стремится.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

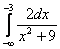
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.