Метод решения несобственного интеграла второго рода с точками разрыва на обоих концах отрезка

Заключительные пункты этой статьи предназначены для читателей, которые хорошо разобрались с несобственными интегралами второго рода на уроке Несобственные интегралы. Примеры решений. Рассмотрим другие разновидности несобственных интегралов второго рода. Ничего сложного!

Многие выкладки предыдущего параграфа будет справедливы и сейчас.

Сразу конкретная задача:

Пример 12

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечные разрывы в обоих концах отрезка интегрирования. Изобразим подынтегральную функцию

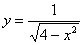
на чертёже:

Геометрически данный несобственный интеграл представляет собой площадь бесконечной криволинейной трапеции, которая не ограничена сверху.

Методика решения практически такая же, как и в предыдущем параграфе. Представим несобственный интеграл в виде суммы двух несобственных интегралов:

Если оба интеграла правой части сходятся, то сходится и весь интеграл.
Если хотя бы одиниз интегралов правой части расходится, то расходится и весь интеграл

А уж интегралы правой части рассматривались во втором разделе урока Несобственные интегралы. Примеры решений.

Но, вместо этого замечаем, что подынтегральная функция является чётной. Чётность использовать МОЖНО. В этом легко убедиться и по чертежу. Таким образом, интеграл целесообразно споловинить, а результат удвоить. Решаем наиболее рациональным способом:

Подынтегральная функция терпит бесконечные разрывы в точках . Данная функция является чётной, а интервал интегрирования симметричен относительно нуля.

Ответ:

,

то есть, несобственный интеграл сходится

Пример 13

Вычислить несобственный интеграл или установить его расходимость.

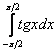
Это пример для самостоятельного решения. Всё, как и в предыдущем параграфе –нечетностью функции пользоваться НЕ НУЖНО. Аккуратно делим интеграл на две части и исследуем сходимость по типовому алгоритму. Полное решение и ответ в конце урока.

Не редкость, когда подынтегральная функция не является четной или нечетной, да и отрезок интегрирования не симметричен относительно нуля. Например, рассмотрим несобственный интеграл

.

Подынтегральная функция опять терпит бесконечные разрывы в обоих концах отрезка интегрирования. Алгоритм такой же, делим интеграл на два интеграла:

Удобное свойство, правда?

Интегралы правой части разобраны на уроке Несобственные интегралы. Примеры решений. Если оба интеграла будут сходиться, то будет сходиться и весь интеграл. Еслихотя бы один интеграл правой части расходится, то расходится и весь интеграл.

Кстати, не важно, в каком порядке исследовать сходимость интегралов правой части. Можно сначала исследовать сходимость интеграла

,

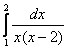а потом (если до этого дойдет дело), исследовать сходимость первого интеграла в правой части.