Как вычислить определенный интеграл методом трапеций?

Сначала формула в общем виде. Возможно, она будет не всем и не сразу понятна… да Карлссон с вами – практические примеры всё прояснят! Спокойствие. Только спокойствие.

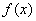Рассмотрим определенный интеграл , где – функция, непрерывная на отрезке . Проведём разбиение отрезка на 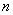равных отрезков:
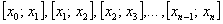. При этом, очевидно: (нижний предел интегрирования) и (верхний предел интегрирования). Точки также называют узлами.

Тогда определенный интеграл можно вычислить приближенно по формуле трапеций:
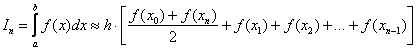, где:
– длина каждого из маленьких отрезков или шаг;
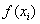– значения подынтегральной функции в точках .

Пример 1

Вычислить приближенно определенный интеграл по формуле трапеций. Результаты округлить до трёх знаков после запятой.

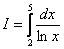
а) Разбив отрезок интегрирования на 3 части.
б) Разбив отрезок интегрирования на 5 частей.

Решение:
а) Специально для чайников я привязал первый пункт к чертежу, который наглядно демонстрировал принцип метода. Если будет трудно, посматривайте на чертёж по ходу комментариев, вот его кусок:

По условию отрезок интегрирования нужно разделить на 3 части, то есть .
Вычислим длину каждого отрезка разбиения: . Параметр 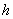, напоминаю, также называется шагом.

Сколько будет точек 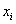(узлов разбиения)? Их будет на одну больше, чем количество отрезков:

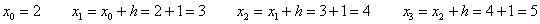
Таким образом, общая формула трапеций сокращается до приятных размеров:

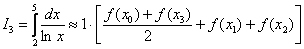
Для расчетов можно использовать обычный микрокалькулятор:

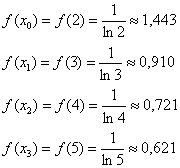
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-его знака после запятой.

Окончательно:

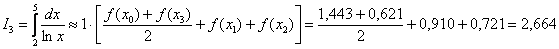
Напоминаю, что полученное значение – это приближенное значение площади (см. рисунок выше).

б) Разобьём отрезок интегрирования на 5 равных частей, то есть 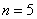. Зачем это нужно? Чтобы Фобос-Грунт не падал в океан – увеличивая количество отрезков, мы увеличиваем точность вычислений.

Если 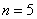, то формула трапеций принимает следующий вид:

Найдем шаг разбиения:
, то есть, длина каждого промежуточного отрезка равна 0,6.

При чистовом оформлении задачи все вычисления удобно оформлять расчетной таблицей:

В первой строке записываем «счётчик»

Как формируется вторая строка, думаю, всем видно – сначала записываем нижний предел интегрирования 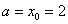, остальные значения получаем, последовательно приплюсовывая шаг .

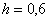По какому принципу заполняется нижняя строка, тоже, думаю, практически все поняли. Например, если 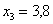, то 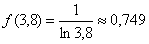. Что называется, считай, не ленись.

В результате:

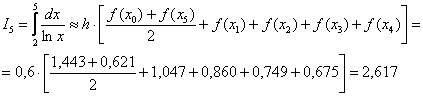
Ну что же, уточнение, и серьёзное, действительно есть!
Если для 3-х отрезков разбиения 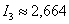, то для 5-ти отрезков 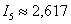. Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере .

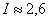Пример 2

Вычислить приближенно определенный интеграл по формуле трапеций с точностью до двух знаков после запятой (до 0,01).

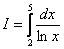
Решение: Почти та же задача, но немного в другой формулировке. Принципиальное отличие от Примера 1 состоит в том, что мы не знаем, НА СКОЛЬКО отрезков разбивать отрезок интегрирования, чтобы получить два верных знака после запятой. Иными словами, мы не знаем значение .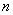

Существует специальная формула, позволяющая определить количество отрезков разбиения, чтобы гарантированно достигнуть требуемой точности, но практике она часто трудноприменима. Поэтому выгодно использовать упрощенный подход.

Сначала отрезок интегрирования разбивается на несколько больших отрезков, как правило, на 2-3-4-5. Разобьем отрезок интегрирования, например, на те же 5 частей. Формула уже знакома:

И шаг, естественно, тоже известен:

Но возникает еще один вопрос, до какого разряда округлять результаты 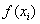? В условии же ничего не сказано о том, сколько оставлять знаков после запятой. Общая рекомендация такова: к требуемой точности нужно прибавить 2-3 разряда. В данном случае необходимая точность 0,01. Согласно рекомендации, после запятой для верности оставим пять знаков (можно было и четыре):

В результате:

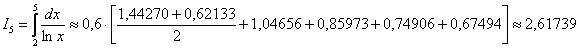
После первичного результата количество отрезков удваивают. В данном случае необходимо провести разбиение на 10 отрезков. И когда количество отрезков растёт, то в голову приходит светлая мысль, что тыкать пальцами в микрокалькулятор уже как-то надоело. Поэтому еще раз предлагаю закачать и использовать мой калькулятор-полуавтомат (ссылка в начале урока).

Для формула трапеций приобретает следующий вид:

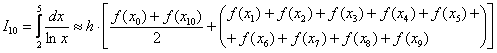
В бумажной версии запись можно спокойно перенести на следующую строчку.

Вычислим шаг разбиения: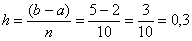

Результаты расчётов сведём в таблицу:

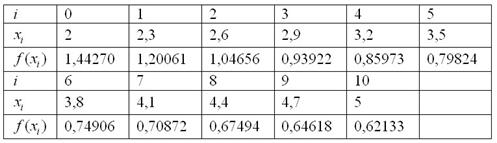
При чистовом оформлении в тетрадь длинную таблицу выгодно превратить в двухэтажную.

В результате:

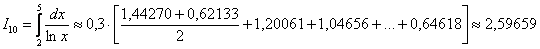
Теперь рассчитаем, на сколько улучшился результат:

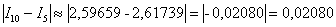
Здесь используем знак модуля, поскольку нас интересует абсолютная разность, а не какой результат больше, а какой – меньше.

Полученная оценка погрешности больше, чем требуемая точность:

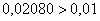
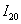Поэтому необходимо ещё раз удвоить количество отрезков разбиения до , и вычислить уже . Ничего не придумываю, в реальных задачах достаточно часто требуется провести разбиение отрезка на 20 частей. С помощью экселевского калькулятора готовый результат можно получить в считанные секунды: .

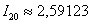Снова оцениваем погрешность:

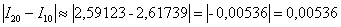
Полученная оценка погрешности меньше, чем требуемая точность:

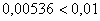
Всё что осталось сделать, округлить последний (наиболее точный) результат 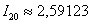до двух знаков после запятой и записать:

Ответ: 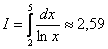с точностью до 0,01

Пример 3

Вычислить приближенно определенный интеграл по формуле трапеций с точностью до 0,001.

Перед вами опять неберущийся интеграл (почти интегральный косинус). В образце решения на первом шаге проведено разбиение на 4 отрезка, то есть 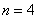. Полное решение и примерный образец чистового оформления в конце урока.