В неопределенном интеграле нередко ответ можно записать несколькими способами

В только что рассмотренном примере окончательный ответ 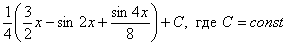можно было записать иначе – раскрыть скобки и даже это сделать еще до интегрирования выражения, то есть вполне допустима следующая концовка примера:

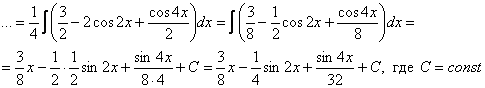
Вполне возможно, что такой вариант даже удобнее, просто я объяснил так, как сам привык решать). Вот еще один характерный пример для самостоятельного решения:

Пример 10

Найти неопределенный интеграл.

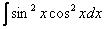
Это пример решается двумя способами, и у Вас могут получиться два совершенно разных ответа (точнее говоря, они будут выглядеть совершенно по-разному, а с математической точки зрения являться эквивалентными). Скорее всего, Вы не увидите наиболее рациональный способ и помучаетесь с раскрытием скобок, использованием других тригонометрических формул. Наиболее эффективное решение приведено в конце урока.

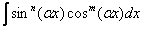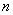Подытоживая параграф, сделаем вывод: любой интеграл вида , где и 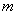– чётные числа, решается методом понижения степени подынтегральной функции.
На практике мне встречались интегралы с 8 и 10 степенями, решать их ужасный геморприходилось, понижая степень несколько раз, в результате чего получались длинные-длинные ответы.