Общий ориентир: в похожих случаях за нужно обозначить функцию, которая находится в знаменателе.
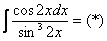
Прерываем решение и проводим замену
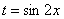
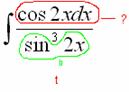
В знаменателе у нас всё хорошо, всё зависит только от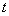 
, теперь осталось выяснить, во что превратится 
.
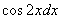Для этого находим дифференциал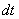 
:
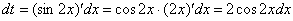
Или, если короче: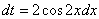 
Из полученного равенства по правилу пропорции выражаем нужное нам выражение:
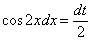
Итак:
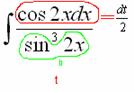
Теперь всё подынтегральное выражение у нас зависит только от 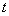и можно продолжать решение
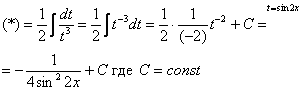
Готово. Напоминаю, что цель замены – упростить подынтегральное выражение, в данном случае всё свелось к интегрированию степенной функции по таблице.
Я не случайно так подробно расписал этот пример, это сделано в целях повторения и закрепления материалов урока Метод замены переменной в неопределенном интеграле.
А сейчас два примера для самостоятельного решения:
Пример 12
Найти неопределенный интеграл.
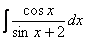
Пример 13
Найти неопределенный интеграл.
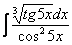
Полные решения и ответы в конце урока.
Пример 14
Найти неопределенный интеграл.
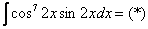
Здесь опять в подынтегральном выражении находятся синус с косинусом (функция с производной), но уже в произведении, и возникает дилемма – что же обозначать за 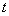, синус или косинус?
Можно попытаться провести замену методом научного тыка, и, если ничего не получится, то обозначить за 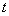другую функцию, но есть:
Общий ориентир: за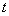 нужно обозначить ту функция, которая, образно говоря, находится в «неудобном положении».
Мы видим, что в данном примере студент косинус «мучается» от степени, а синус – свободно так сидит, сам по себе.
Поэтому проведем замену:
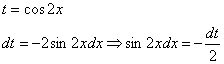
Если у кого остались трудности с алгоритмом замены переменной и нахождением дифференциала 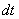, то следует вернуться к уроку Метод замены переменной в неопределенном интеграле.
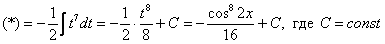
Пример 15
Найти неопределенный интеграл.
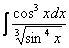
Анализируем подынтегральную функцию, что нужно обозначить за ?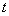
Вспоминаем наши ориентиры:
1) Функция, скорее всего, находится в знаменателе;
2) Функция находится в «неудобном положении».
Кстати, эти ориентиры справедливы не только для тригонометрических функций.
Под оба критерия (особенно под второй) подходит синус, поэтому напрашивается замена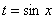 
. В принципе, замену можно уже проводить, но сначала неплохо было бы разобраться, а что делать с 
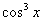? Во-первых, «отщипываем» один косинус:
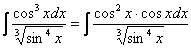
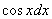мы резервируем под наш «будущий» дифференциал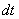
А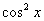 
выражаем через синус с помощью основного тригонометрического тождества:
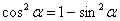
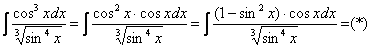
Вот теперь замена: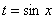
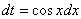
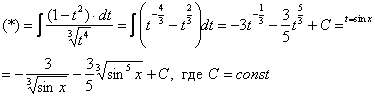
Готово.
Общее правило: Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится внечетнойстепени, то нужно от нечетной степени «откусить» одну функцию, а за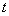 – обозначить другую функцию.Речь идет только об интегралах, где есть косинусы и синусы.
В рассмотренном примере в нечетной степени у нас находился косинус, поэтому мы отщипнули от степени один косинус, а за 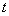обозначили синус.
Пример 16
Найти неопределенный интеграл.
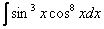
Степени идут на взлёт =).
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
Дата добавления: 2014-11-29; просмотров: 1614;