Автономный (общий) риск в сравнении с рыночным риском.
Рисковость отдельно взятого актива представляет собой общий риск. Рыночный риск представляет собой релевантный, или эффективный, риск отдельного актива, если данный актив является частью хорошо диверсифицированного портфеля ценных бумаг. Общий риск акций измеряется дисперсией возможных значений доходности относительно их средней величины. Чем больше разброс, тем выше вероятность того, что фактическая доходность окажется ниже ожидаемой, и, следовательно, тем выше риск этой величины.
Релевантный риск акции – это ее рыночный риск, который измеряет долю каждой акции в общем риске портфеля. Чем больше воздействие акции на общий риск портфеля (увеличение количества акции данного вида увеличивает риск портфеля), тем выше рыночный риск акции.
На рыночный риск акции оказывают воздействие ее общий риск, а также корреляция между доходностью данной акции и доходностью всего портфеля ценных бумаг.
Коэффициент корреляции – нормализованная статистическая мера линейного соотношения двух переменных. Она принимает значение в диапазоне от -1,0 (полная отрицательная корреляция ) через 0 (отсутствие корреляции) до +1,0 (полная положительная корреляция).
Коэффициент корреляции принимает значение в диапазоне от -1,0 до +1,0. Положительный коэффициент корреляции говорит о том, что в общем случае движение доходностей ценных бумаг происходит в одном направлении, а отрицательный – в противоположных. Чем сильнее взаимосвязь, тем ближе коэффициент корреляции к одному из крайних значений. Нулевой коэффициент корреляции свидетельствует о том, что доходности двух ценных бумаг не коррелированы, т.е. не наблюдается тенденции их совместного изменения (положительной или отрицательной).
Анализ автономного риска : активы рассматриваемые изолированно. Расчет ожидаемого значения доходности актива. В статистике количественным измерителем степени разброса значений переменной вокруг ее средней величины (математического ожидания) является показатель дисперсии (δ2), который определяется по формуле:
δ2= 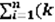 i -
i - 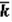 )2pi
)2pi
где:δ2- дисперсия;
ki- i-й возможный исход;
pi – вероятность появления i-го исхода;
n - число исходов
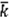 –средняя ожидаемая доходность
–средняя ожидаемая доходность
Квадратный корень из дисперсии называется средним квадратическим или стандартным отклонением δ:
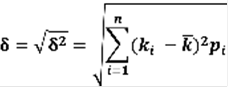
Дата добавления: 2014-12-27; просмотров: 5000;
