Модель Марковитца

Основная идея модели Марковитца заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную, т.е. доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. Для упрощения модель Марковитца полагает, что доходы по альтернативам инвестирования распределены нормально.

По модели Марковитца определяются показатели, характеризующие объем инвестиций и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.

В качестве масштаба ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.

Пусть формируется портфель из п ценных бумаг. Ожидаемое значение дохода по i-й ценной бумаге (Еi) рассчитывается как среднеарифметическое из отдельных возможных доходов Ri с весами Рij, приписанным им вероятностями наступления:

,

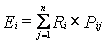Где :сумма Рij = 1;

n—задает количество оценок дохода по каждой ценной бумаге.

Для измерения риска служат показатели рассеивания, поэтому чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен. Таким образом, риск выражается отклонением (причем более низких!) значений доходов от наиболее вероятного значения. Мерой рассеяния является среднеквадратичное отклонен si и, чем больше это значение, тем больше риск:

.

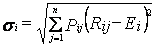В модели Марковитца для измерения риска вместо среднеквадратичного отклонения используется дисперсия Di, равная квадрату si, так как этот показатель имеет преимущества по технике расчетов.

Инвестора, желающего оптимально вложить капитал, интересует не столько сравнение отдельных видов ценных бумаг между собой, сколько сравнение всевозможных портфелей, так как это позволяет использовать эффект рассеивания риска, т.е. определяется ожидаемое значение дохода и дисперсия портфеля. Ожидаемое значение дохода Е портфеля ценных бумаг определяется как сумма наиболее вероятных доходов Еi, различных ценных бумаг n. При этом доходы взвешиваются с относительными долями Xi (i = 1....n), соответствующими вложениям капитала в каждую облигацию или акцию:

.

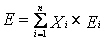Для дисперсии эта сумма применима с определенными ограничениями, так как изменение курса акций на рынке происходит не изолированно друг от друга, а охватывает весь рынок в целом. Поэтому дисперсия зависит не только от степени рассеяния отдельных ценных бумаг, а также от того, как все ценные бумаги в совокупности одновременно понижаются или повышаются по курсу, т.е. от корреляции между изменениями курсов отдельных ценных бумаг. При сильной корреляции между отдельными курсами (т.е. если все акции одновременно повышаются или понижаются) риск за счет вкладов в различные ценные бумаги нельзя ни уменьшить, ни увеличить. Если же курсы акций абсолютно не коррелируют между собой, но в предельном случае (портфель содержит бесконечное число акций) риск можно было бы исключить полностью, так как колебания курсов в среднем были бы равны нулю. На практике число ценных бумаг в портфеле всегда конечно, и поэтому распределение инвестиций по различным ценным бумагам может лишь уменьшить риск, но полностью его исключить невозможно.

Итак, при определении риска конкретного портфеля ценных бумаг необходимо учитывать корреляцию курсов акций. В качестве показателя корреляции Марковитц использует ковариацию Qk между изменениями курсов отдельных ценных бумаг.

Таким образом, дисперсия всего портфеля рассчитывается по следующей формуле:

.

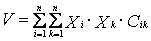По определению для i = k Сik равно дисперсии акции. Это означает, что дисперсия, а значит, и риск данного портфеля зависят от риска данной акции, ковариации между отдельными акциями (т.е. систематического риска рынка) и долей Xi отдельных ценных бумаг в портфеле в целом.

Рассматривая теоретически предельный случай, при котором в портфель можно включать бесконечное количество ценных бумаг, дисперсия асимптотически будет приближаться к среднему значению ковариации С. Графически это можно представить в следующем виде на рисунке 1.

Итак, Марковитц разработал очень важное для современной теории портфеля ценных бумаг положение, которое гласит: совокупный риск портфеля можно разложить на две составные части. С одной стороны, это так называемый систематический риск, который нельзя исключить и которому подвержены все ценные бумаги практически в равной степени. С другой — специфический риск для каждой конкретной ценной бумаги, который можно избежать при помощи управления портфелем ценных бумаг. При этом сумма сложенных средств по всем объектам должна быть равна общему объему инвестиционных вложений (например, часть средств на банковском счете вводится в модель как инвестиция с нулевым риском), т. е. сумма относительных долей Xi в общем объеме должна равняться единице:

.

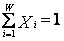Проблема заключается в численном определении относительных долей акций и облигаций в портфеле (значений Xi), которые наиболее выгодны для владельца. Марковитц ограничивает решение модели тем, что из всего множества «допустимых» портфелей, т. е. удовлетворяющих ограничениям необходимо выделить те, которые рискованнее, чем другие. Это портфели содержащие при одинаковом доходе больший риск (дисперсию) по сравнению с другими, или портфели, приносящие меньший доход при одинаковое уровне риска.

При помощи разработанного Марковитцем метода критических линий можно выделить неперспективные портфели, не удовлетворяющие ограничениям. Тем самым остаются только эффективные портфели, т. е. портфели содержащие минимальный риск при заданном доходе или приносящих максимально возможный доход при заданном максимальном уровне риска на который может пойти инвестор.

Данный факт имеет очень большое значение в современной теории портфелей ценных бумаг. Отобранные таким образом портфели объединяют в список, содержащий сведения о процентном составе портфеля и отдельных ценных бумаг, а также о доходе и риске портфелей. Выбор конкретного портфеля зависит от максимального риска, на который готов пойти инвестор.

На рисунке 2 представлены недопустимые, допустимые и эффективные портфели. Портфель является эффективным, если он удовлетворяет ограничениям, и, кроме того, для заданного дохода, например, Е1 содержит меньший риск R1 по сравнению с другими портфелями, приносящими такой же доход Е1, или при определенном риске R2 приносит более высокий доход Е2 по сравнению с другими комбинациями с R2.

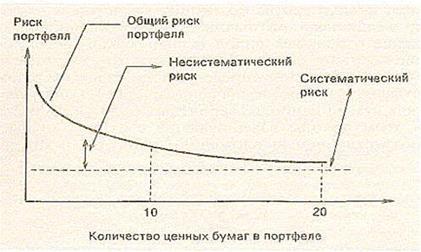
Рисунок1. Возможность уменьшения риска при помощи управления портфелем ценных бумаг

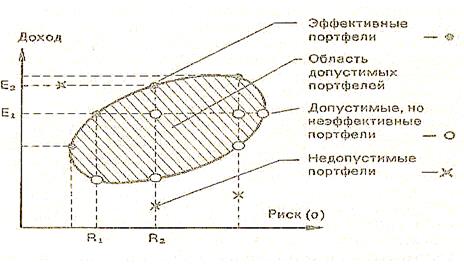
Рисунок 2. Недопустимые, допустимые и эффективные портфели

С методологической точки зрения модель Марковитца можно определить как практически-нормативную, что, конечно, не означает навязывание инвестору определенного стиля поведения на рынке ценных бумаг. Задаче модели заключается в том, чтобы показать, как поставленные цели достижимы на практике.