Интегралы от тригонометрических функций. Примеры решений

На данном уроке мы рассмотрим интегралы от тригонометрических функций, то есть начинкой интегралов у нас будут синусы, косинусы, тангенсы и котангенсы в различных комбинациях. Все примеры будут разобраны подробно, доступно и понятно даже для чайника.

Для успешного изучения интегралов от тригонометрических функций Вы должны хорошо ориентироваться в простейших интегралах, а также владеть некоторыми приемами интегрирования. Ознакомиться с этими материалами можно на лекциях Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.

А сейчас нам потребуются: Таблица интегралов, Таблица производных и Справочник тригонометрических формул. Все методические пособия можно найти на страницеМатематические формулы и таблицы. Рекомендую всё распечатать. Особо заостряю внимание на тригонометрических формулах, они должны быть перед глазами – без этого эффективность работы заметно снизится.

Но сначала о том, каких интегралов в данной статье нет. Здесь не найдется интегралов вида 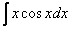, 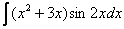– косинус, синус, умноженный на какой-нибудь многочлен (реже что-нибудь с тангенсом или котангенсом). Такие интегралы интегрируются по частям, и для изучения метода посетите урок Интегрирование по частям. Примеры решений.Также здесь не найдется интегралов с «арками» – арктангенсом, арксинусом и др., они тоже чаще всего интегрируются по частям.

При нахождении интегралов от тригонометрических функций используется ряд методов: