Интегралы от экспоненты, умноженной на многочлен
Общее правило: за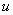 всегда обозначается многочлен
всегда обозначается многочлен
Пример 5
Найти неопределенный интеграл.
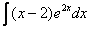
Решение:
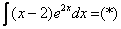
Используя знакомый алгоритм, интегрируем по частям:

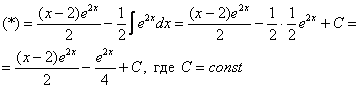
Если возникли трудности с интегралом 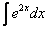 , то следует вернуться к статье Метод замены переменной в неопределенном интеграле.
, то следует вернуться к статье Метод замены переменной в неопределенном интеграле.
Единственное, что еще можно сделать, это «причесать» ответ:
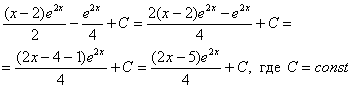
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом 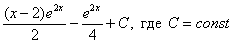 или даже
или даже 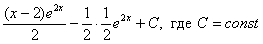
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Пример 6
Найти неопределенный интеграл.
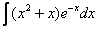
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что  – сложная функция.
– сложная функция.
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Дата добавления: 2014-11-29; просмотров: 2643;
