Интеграл от неразложимого многочлена 2-ой степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Пример 13
Найти неопределенный интеграл
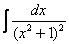
В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваю, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
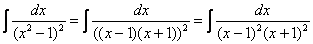 – и далее применяется стандартный метод неопределенных коэффициентов.
– и далее применяется стандартный метод неопределенных коэффициентов.
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:

Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:
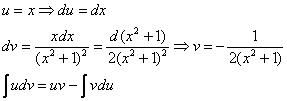
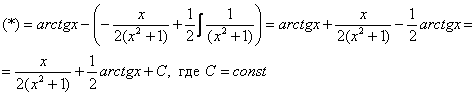
Готово.
Для интеграла вида 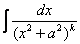 (
( 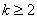 – натуральное число) выведена рекуррентнаяформула понижения степени:
– натуральное число) выведена рекуррентнаяформула понижения степени:
 , где
, где 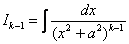 – интеграл степенью ниже.
– интеграл степенью ниже.
Убедимся в справедливости данной формулы для прорешанного интеграла 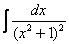 .
.
В данном случае: 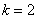 ,
,  , используем формулу:
, используем формулу:
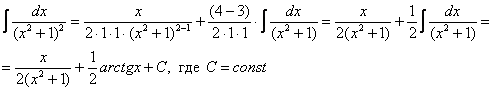
Как видите, ответы совпадают.
Пример 14
Найти неопределенный интеграл
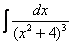
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
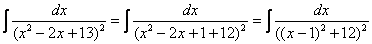
Далее следует «безболезненная» линейная замена 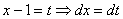 и получается знакомый интеграл
и получается знакомый интеграл 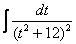 .
.
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу, поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции, пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Дата добавления: 2014-11-29; просмотров: 2267;
