Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Пример 9
Найти неопределенный интеграл
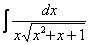
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
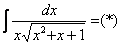
Замена тут проста:
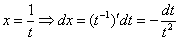
Смотрим на жизнь после замены:
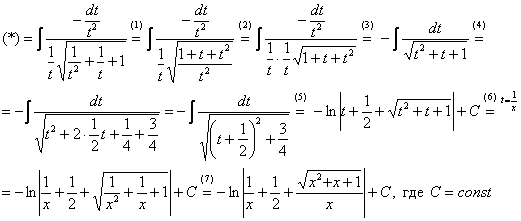
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим 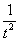 из-под корня.
из-под корня.
(3) Числитель и знаменатель сокращаем на 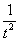 . Заодно под корнем я переставил слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
. Заодно под корнем я переставил слагаемые в удобном порядке. При определенном опыте шаги (1), (2) можно пропускать, выполняя прокомментированные действия устно.
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально 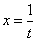 , то обратно:
, то обратно: 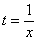 .
.
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня  .
.
Пример 10
Найти неопределенный интеграл
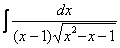
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же:
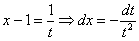
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены: 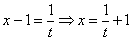
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Пример 11
Найти неопределенный интеграл
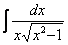
Пример 12
Найти неопределенный интеграл
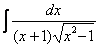
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, метод решения которого рассматривался на урокеИнтегралы от иррациональных функций.
Дата добавления: 2014-11-29; просмотров: 2345;
