Интегрирование по частям
Метод заключается в применении формулы интегрирования по частям
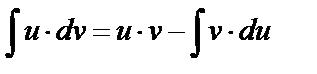
Смысл этой формулы состоит в том, чтобы в результате её применения интеграл в правой её части оказался проще первоначального. Для применения формулы интегрирования по частям подынтегральное выражение следует разбить на два множителя. Один из них обозначается через 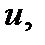 а остальная часть (содержащая
а остальная часть (содержащая 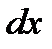 ) относится ко второму множителю и обозначается через
) относится ко второму множителю и обозначается через 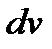 . Затем дифференцированием находится
. Затем дифференцированием находится 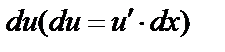 и интегрированием - функция
и интегрированием - функция 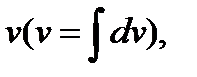 причем в
причем в 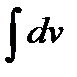 произвольная постоянная
произвольная постоянная 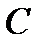 берётся равной нулю.
берётся равной нулю.
Пример 16.
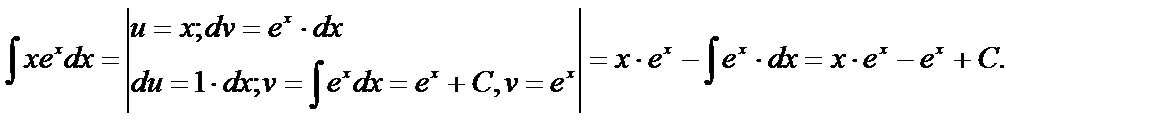
Пример 17.
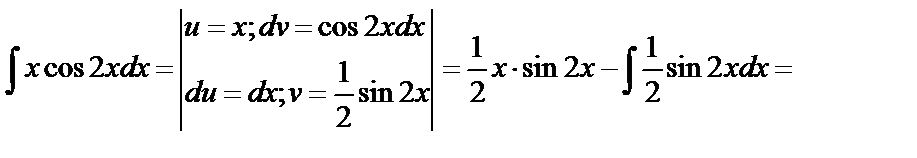
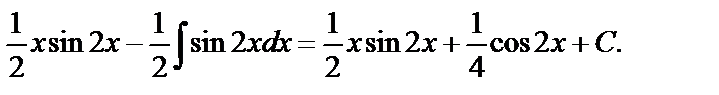
Пример 18.
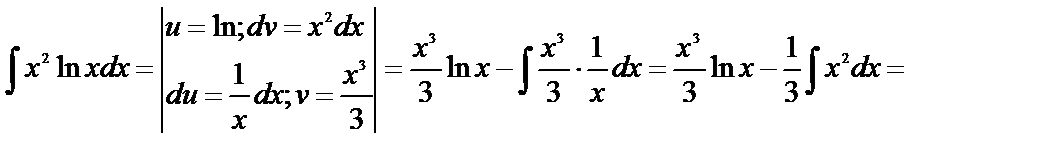
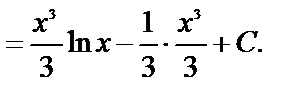
Пример 19.
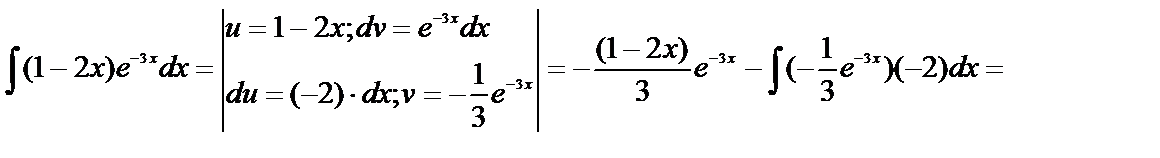
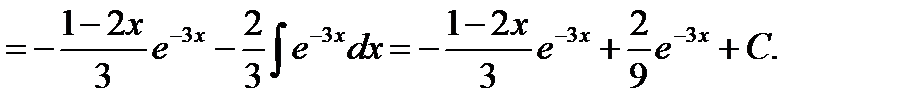
Пример 20.
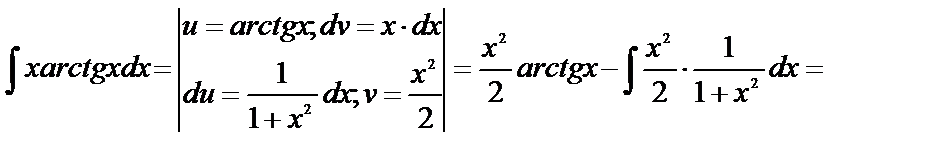
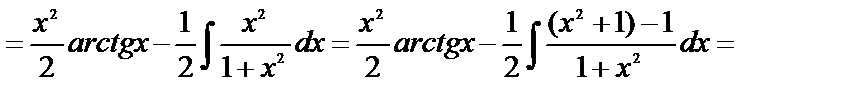
= 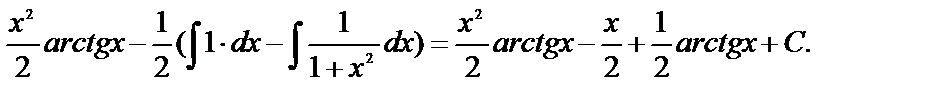
Пример 21.
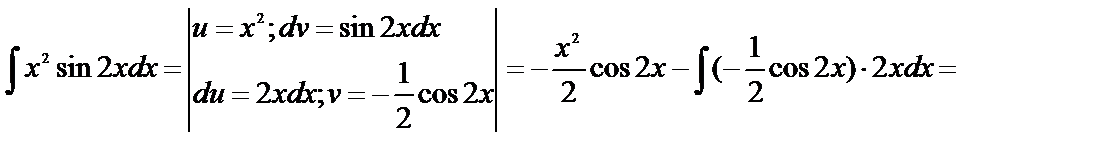
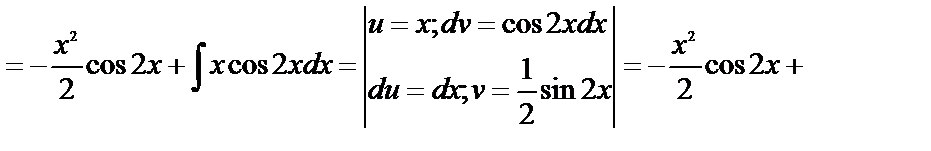
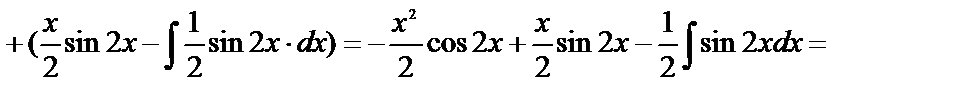
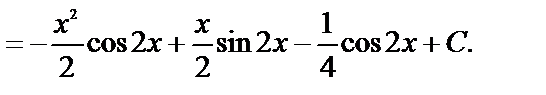
Формула интегрирования по частям применяется к интегралам следующего вида:
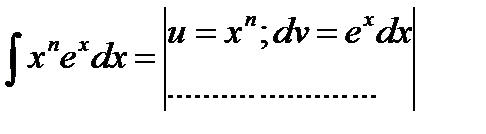
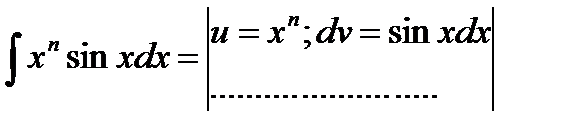
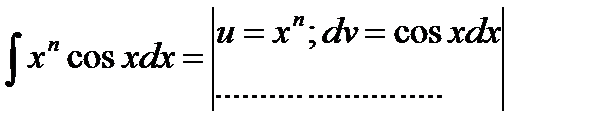
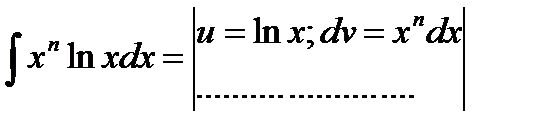

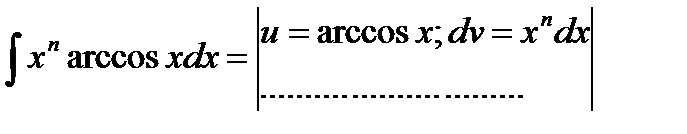

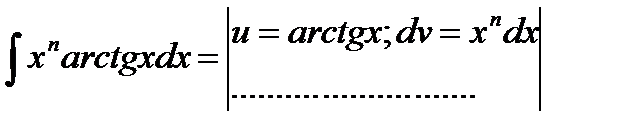
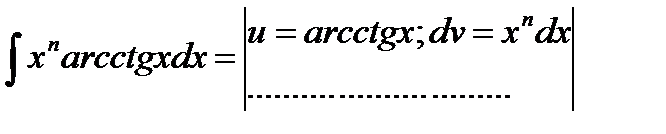
Дата добавления: 2014-12-30; просмотров: 960;
