Замена переменной и формула интегрирования по частям в определенном интеграле

Теорема 1. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а= φ(α), b= φ(β) и функция f(x) непрерывна в каждой точке х вида х= φ(t), где t 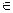[α,β].

Тогда справедливо равенство

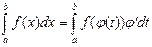
Это формула замены переменной в определенном интеграле.

При этом в отличие от неопределенного интеграла нет необходимости возвращаться к исходной переменной интегрирования, достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение уравнений φ(t)= а и φ(t)=b.

Теорема 2.Пусть функции u = u(x) и = v(x) имеют непрерывные производные на отрезке [a,b]. Тогда

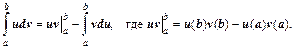
Это формула интегрирования по частям для определенного интеграла.

Пример 1. Вычислить интеграл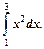

Р е ш е н и е. Для подынтегральной функции y=x² произвольная первообразная имеет вид: 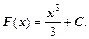Так как в формуле Ньютона-Лейбница можно использовать любую первообразную, то для вычисления интеграла возьмем первообразную, имеющую наиболее простой вид: 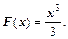Тогда

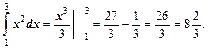
Пример 2. Вычислить интеграл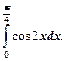

Р е ш е н и е. По формуле Ньютона-Лейбница имеем:

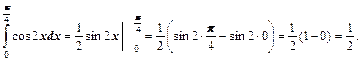
Пример 3. Вычислить определенный интеграл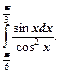

Р е ш е н и е. Используя метод замены переменной, перейдем к другой переменной 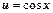, тогда 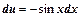, значит 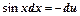. Пересчитаем пределы интегрирования для новой переменной : ; .

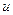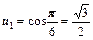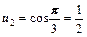Запишем интеграл с новой переменной :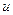

.

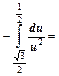
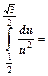
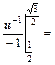
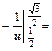
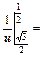
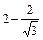Пример 4. Вычислить определенный интеграл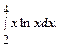

Р е ш е н и е. Используя метод интегрирования по частям, получим:

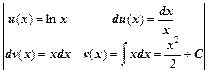
Тогда

.

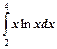
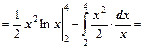
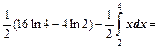
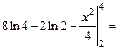
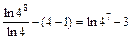Пример 5. Вычислить площадь фигуры, ограниченной линиями 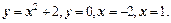Площадь криволинейной трапеции, представленная на рис.7 будет равна определенному интегралу от функции - y=x²+2 в интервале [-2;1]:

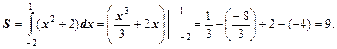
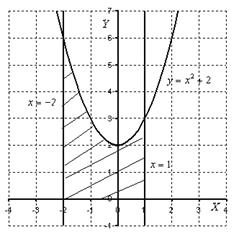
Рис.7