Интегрирование рациональной дроби.

Задача интегрирования сводится к интегрированию простейших дробей следующих четырех типов:

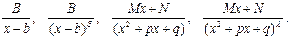
Здесь β=2, 3, …; λ=2, 3, …; B, M, N, b, p и q – некоторые вещественные числа, причем трехчлен x²+px+q не имеет вещественных корней, т.е. q-p²/4>0.

При этом справедлива следующая теорема:

Теорема.Всякая рациональная дробь интегрируема в элементарных функциях.

Действительно, если произвести подстановку t=x-b, то дроби первого и второго типа будут интегрируемы в элементарных функциях т. е.:

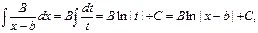
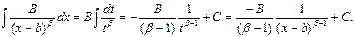
Квадратные трехчлены третьей и четвертой дробей можно представить в виде (x²+px+q)=(x+p/2)²+(q-p²/4) и, учитывая, что (q-p²/4)>0, ввести вещественную постоянную 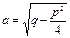и сделать подстановку t=x+p/2, тогда задача интегрирования может быть решена с использованием известных формул интегрирования.