Интегрирование по частям. Формула интегрирования получается почленным интегрированием формулы производной произведения.
Формула интегрирования получается почленным интегрированием формулы производной произведения.
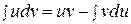 .
.
Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный.
Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям.
I. 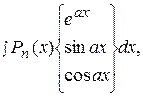
где 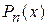 - многочлен степени
- многочлен степени 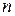 . В качестве
. В качестве 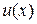 нужно взять
нужно взять 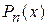 , а
, а 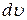 =
= 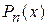 - другой сомножитель.
- другой сомножитель.
При этом формулу приходится применить столько раз, какова степень многочлена.
II. 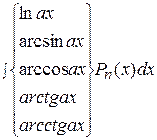 .
.
В этом случае, наоборот, следует положить 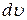 =
= 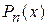 .
.
Рассмотрим применение указанной схемы.
Пример 13.
 .
.
Это интеграл первого типа, поэтому:
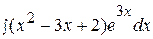 =
= 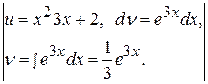 =
=
= 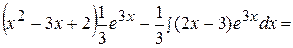
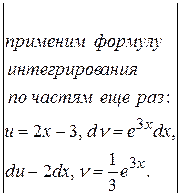 =
=
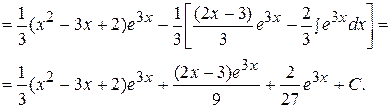
Пример 14. 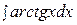 .
.
Решение.
Это интеграл второго типа, поэтому имеем:
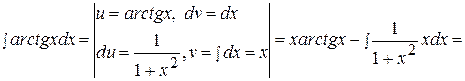
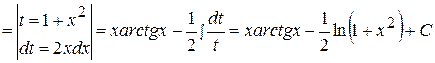 .
.
Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию  по ее дифференциалу
по ее дифференциалу 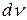 . Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
. Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
Формула интегрирования по частям может хорошо сработать и в других случаях.
Пример 15 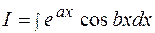 .
.
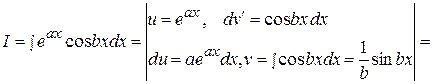
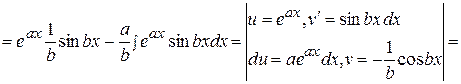
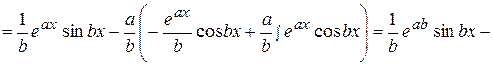
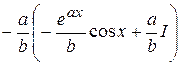 .
.
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим
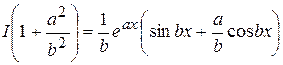 ,
,
откуда
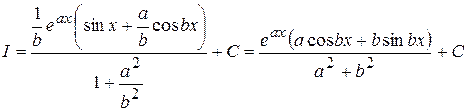 .
.
Дата добавления: 2014-12-08; просмотров: 981;
