Метод замены переменного
Пусть требуется найти неопределенный интеграл от непрерывной функции 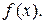
Рассмотрим некоторую функцию 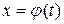 , которая имеет непрерывную производную
, которая имеет непрерывную производную  и обратную функцию
и обратную функцию 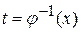 . (Например:
. (Например: 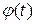 монотонна). Тогда справедлива формула:
монотонна). Тогда справедлива формула:
 . (4.1.1)
. (4.1.1)
В некоторых ситуациях удается подобрать функцию 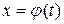 так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
так, что интеграл в правой части (3.1.1) оказывается проще, чем в левой части. Такой прием называется методом замены переменной. На практике часто формулу используют в обратную сторону:
 . (4.1.2)
. (4.1.2)
Другими словами, если подынтегральное выражение может быть записано в форме левой части (4.1.2), то с помощью подстановки 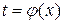 получаем более простой интеграл (4.1.1).
получаем более простой интеграл (4.1.1).
Пример 8 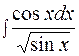 .
.
Решение.
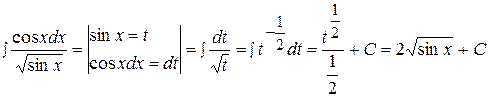 .
.
Пример 9 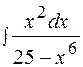 .
.
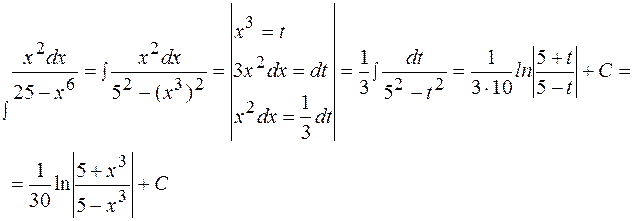
На практике часто используется следующая простая формула:
 ,
,
где 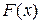 - первообразная функции
- первообразная функции 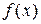 .
.
Пример 10.  .
.
Пример 11. 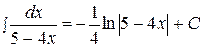 .
.
Пример 12. 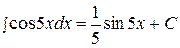 .
.
Дата добавления: 2014-12-08; просмотров: 850;
