Интегрирование выражений, содержащих квадратный трехчлен.

К этому типу интегралов относятся интегралы вида:

;

;

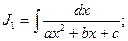
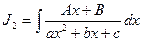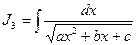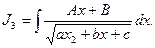
Мы увидим в дальнейшем, что без умения находить такие интегралы, мы не сможем вычислять интегралы от рациональных дробей.

Сначала научимся находить более простые интегралы видов 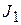и .

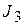Трудность заключается в наличии слагаемого bx. Если бы его не было, то, вынося за знак интеграла 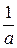, получили бы интеграл вида (11) или (12). Решить проблему можно выделением полного квадрата.

Пример 16 .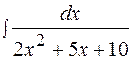

Решение.

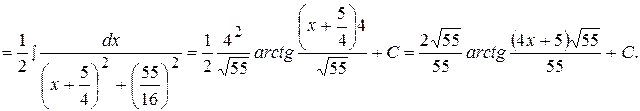
Пример 17 .

Решение.

.

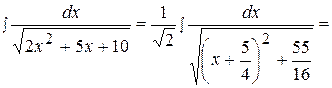
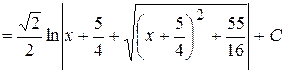Пример 18 .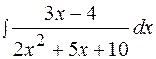

Решение.

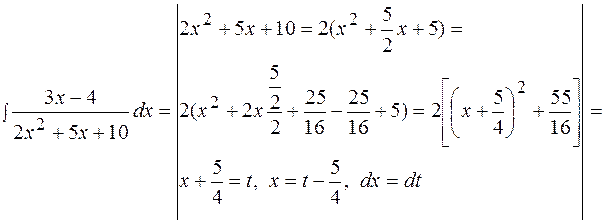
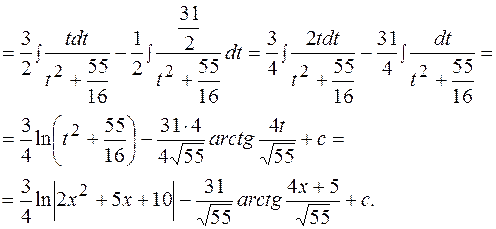
Пример 19 .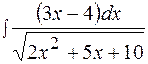

Решение.

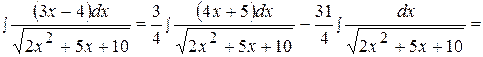
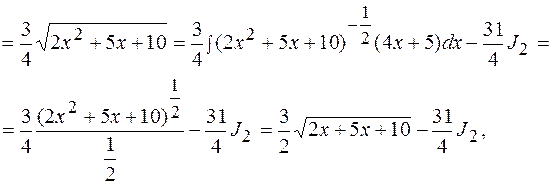
где 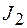- интеграл, рассмотренный в примере 17.