Определенный интеграл.

Теорема. Пусть функция y=f(x) непрерывна на интервале [a,b] и F(x) –любая первообразная для f(x) на [a,b]. Тогда определенный интеграл от функции f(x) на [a,b] равен приращению первообразной F(x) на этом интервале, т. е.

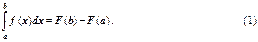
Формула (1) – формула Ньютона-Лейбница. Она утверждает, что определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.

Для вычисления определенного интеграла нужно найти первообразную подынтегральной функции (неопределенный интеграл) и из значения первообразной при верхнем пределе вычесть значение первообразной при нижнем пределе интегрирования.

Геометрический смысл определенного интеграла: это площадь криволинейной трапеции, ограниченной слева прямой х=а, справа прямой x=b, сверху кривой y=f(x), снизу осью Ох.