Тема 6. Дифференциальные уравнения
Обыкновенные дифференциальные уравнения и дифференциальные уравнения n-го порядка.
Обыкновенным дифференциальным уравнением называется уравнение, связывающее искомую функцию, переменную и производные различных порядков данной функции.
В общем случае дифференциальное уравнение можно записать так:
G(x, y, y',…, y(n))=0 , (1)
где G – некоторая функция от n+2 переменных (n >0), при этом n – порядок старшей производной, входящей в запись, называется порядком дифференциального уравнения.
Например, х2у''' - ху' = 0 – обыкновенное дифференциальное уравнение третьего порядка.
Дифференциальное уравнение n-го порядка называется разрешенным относительно старшей производной, если оно имеет вид:
у (n) = F(x, y, y',…, y(n-1)), где F – некоторая функция n+1 переменной.
Решением дифференциального уравнения (1) называется такая функция у = у (х), которая при подстановке её в это уравнение обращает его в тождество. Например, функция у = sin x является решением уравнения у'' + у' = 0, так как (sin x)'' + (sin x)' =0 для любых х.
Задача о нахождении решения некоторого дифференциального уравнения называется задачей интегрирования данного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
Пример 1. Решить уравнение у'' = х.
Р е ш е н и е. Поскольку 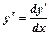 , то исходное уравнение равносильно равенству дифференциалов: dy'=xdx. Выполняя интегрирование левой и правой частей равенства, получим y'=x2/2+ C1, где С1 – произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству dy = (x2/2+C1)dx. Интегрируя обе части равенства, окончательно получаем y=x3/6+ C1x+C2, где С2 – произвольная постоянная.
, то исходное уравнение равносильно равенству дифференциалов: dy'=xdx. Выполняя интегрирование левой и правой частей равенства, получим y'=x2/2+ C1, где С1 – произвольная постоянная. Вновь записывая производную как отношение двух дифференциалов, приходим к равенству dy = (x2/2+C1)dx. Интегрируя обе части равенства, окончательно получаем y=x3/6+ C1x+C2, где С2 – произвольная постоянная.
Отметим, что без дополнительных условий решение данного уравнения неоднозначно.
Общим решением дифференциального уравнения (1) n-го порядка называется такое его решение у = φ (х, С1,… Сn), которое является функцией переменной х и произвольных постоянных C1,C2,…Cn.
Частным решением дифференциального уравнения называется решение, полученное из общего решения при некоторых конкретных числовых значениях постоянных C1,C2,…Cn.
Теорема о существовании и единственности решения дифференциального уравнения I -го порядка
Рассмотрим дифференциальное уравнение первого порядка, разрешенное относительно производной:
у' = f (x,y), (2)
где f – функция двух переменных.
Обозначим через R множество точек плоскости 0ху, на котором функция f (x, y) определена. Пусть R – является открытым множеством, т.е множеством точек плоскости, в котором вместе с каждой точкой содержится и ее окрестность.
Теорема. Пусть в дифференциальном уравнении (2) функция f (x, y) и её частная производная 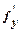 непрерывны на открытом множестве R координатной плоскости 0ху. Тогда справедливы следующие утверждения:
непрерывны на открытом множестве R координатной плоскости 0ху. Тогда справедливы следующие утверждения:
1) Для всякой точки (х0, у0) множества R найдется решение у = у(х) уравнения (2) , удовлетворяющее условию у0 = у(х0).
2) Если два решения у = у1(х) и у = у2(х) уравнения (2) совпадают хотя бы для одного значения х0, т.е. у1(х0) = у2(х0), то эти решения совпадают для всех значений переменной х, для которых они определены.
Пример 2. Решить уравнение у' = у, (3)
Р е ш е н и е. Так как f (x, y) = у и 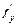 =1, то условия теоремы выполнены (функция f (x,y) и её частная производная
=1, то условия теоремы выполнены (функция f (x,y) и её частная производная 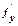 определены и непрерывны на 0ху) и функция у = С ех, где С – число, является решением уравнения (3).
определены и непрерывны на 0ху) и функция у = С ех, где С – число, является решением уравнения (3).
Покажем, что все решения уравнения (3) имеют такой вид при некотором значении постоянной С.
Пусть у=у(х) – некоторое решение уравнения (3), удовлетворяющее условию у0=у(х0). Положим, 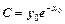 , тогда решения у = у(х) и
, тогда решения у = у(х) и 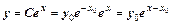 уравнения (3) равны при х=х0 и по теореме совпадают.
уравнения (3) равны при х=х0 и по теореме совпадают.
Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если оно может быть представлено в виде - 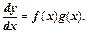
Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функция переменной х окажутся в одной части равенства, а переменная у – в другой. Затем проинтегрировать обе части полученного равенства.
Пример 3. Решить уравнение у' = х(1+2у), y(0)=0 .
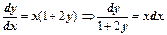
Р е ш е н и е.Это уравнение с разделяющимися переменными:
Выполняя интегрирование, получаем:
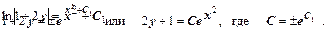
Решение перепишем в виде
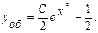
Тогда общее решение данного уравнения имеет вид:
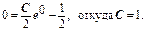
Подставляя в общее решение начальное условие y(0)=0, получим:
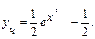 |
Частное решение уравнения найдем из общего, полагая С=1:
Пример 4. Рассмотрим уравнение
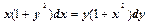 (4.1)
(4.1)
Это уравнение первого порядка с разделяющимися переменными. Разделяя переменные, получим уравнение
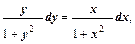 (4.2)
(4.2)
в котором функции (1+y2) и (1+x2) не обращаются в нуль. Поэтому все решения уравнения (4.1) получаются интегрированием уравнения (4.2) и имеют вид 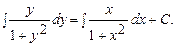
Эти решения можно переписать в виде
ln(1+y2)=ln(1+x2)+lnC1,
где С1- произвольная положительная постоянная.
Окончательно получим, что 1+y2=C1(1+x2).
Дифференциальные уравнения 2-го порядка. Линейные дифференциальные уравнения с постоянными коэффициентами.
В некоторых случаях решение дифференциального уравнения второго порядка может быть сведено к последовательному решению двух дифференциальных уравнений первого порядка (тогда говорят, что данное дифференциальное уравнение допускает понижение порядка).
Если дифференциальное уравнение имеет вид у''=f(х), то оно решается последовательным интегрированием ( см. пример 1).
Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:
y'' + py' + gy = r(x), (4)
где p, g – некоторые действительные числа, r(x) – некоторая функция. Если r(x)=0, то уравнение называется однородным, в противном случае − неоднородным.
Можно доказать, что существует единственное решение уравнения (4), удовлетворяющее начальным условиям у(х0)=z1, у'(х0)=z2, где х0, z1, z2 – некоторые действительные числа.
Рассмотрим сначала решение однородного дифференциального уравнения
y'' + py' + gy = 0. (5)
Будем искать решение этого уравнения в форме
у = еλx, (6)
где λ – некоторое действительное число, если такое существует.
Подставим (6) в (5), получим: (еλx )'' + p(еλx)' + gеλx= (λ2+рλ+g) еλx = 0.
Функция у = еλx является решением уравнения (5), если число λ есть корень уравнения: λ2 + рλ +g = 0, (7) которое называется характеристическим уравнением уравнения (5).
Описание решений уравнения (5) зависит от того, имеет ли соответствующее характеристическое уравнение (7) корни.
Теорема (решение однородного дифференциального уравнения).
1. Пусть характеристическое уравнение (7) имеет два различных действительных корня λ1 и λ2 , тогда общее решение уравнения (5) имеет вид: 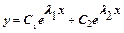 , где С1 и С2 – некоторые числа.
, где С1 и С2 – некоторые числа.
2. Если характеристическое уравнение (7) имеет два одинаковых корня λ , то общее решение уравнения (5) имеет вид:
у = 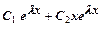 , где С1 и С2 – некоторые числа.
, где С1 и С2 – некоторые числа.
3. Если характеристическое уравнение (7) не имеет действительных корней, то общее решение уравнения (5) имеет вид:
у = 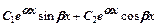 , где
, где 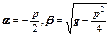 , С1 и С2 – некоторые числа.
, С1 и С2 – некоторые числа.
Перейдем теперь к решению неоднородного уравнения (4) с постоянными коэффициентами.
Это уравнение может быть решено методом вариации произвольных постоянных, который состоит в следующем. Сначала находится общее решение однородного уравнения (5), затем решение уравнения (4) находится в виде у =С1(х)у1+С2(х)у2, т.е. предполагается , что постоянные С1 и С2 являются функциями независимой переменной х. При этом С1(х) и С2(х) могут быть найдены как решения системы
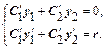
Пример 4. Решить уравнение у'' - 3у' + 2у = ех. (8)
Р е ш е н и е. Решим однородное уравнение у'' - 3у' + 2у =0, для этого составим характеристическое уравнение λ2 - 3λ + 2 = 0 и найдем его корни λ1 =1, λ2 =2.
Тогда общее решение данного уравнения имеет вид:
у = 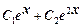 .
.
Полагая теперь, что С1 и С2 являются функциями переменной х, найдем первые производные этих функций, решая систему:
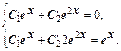
Находим С'1(х) = -1 и С'2(х)= е-х. Полученные дифференциальные уравнения – с разделяющимися переменными. Решая эти уравнения, получаем С1= −х+С3 и С2= −е-х+С4, где С3 и С4 – некоторые постоянные.
Таким образом, окончательно решение уравнения имеет вид:
у = 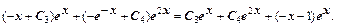
Замечание. Первые два слагаемых – это общее решение однородного уравнения, соответствующего исходному дифференциальному уравнению, последнее – частное решение исходного уравнения (8).
Теорема. Общее решение линейного дифференциального уравнения (4) равно сумме общего решения соответствующего однородного уравнения (5) и частного решения исходного неоднородного уравнения.
В приложении 3. (Дифференциальные уравнения первого порядка) приведены типы дифференциальных уравнений первого порядка и используемые замены и методы их решения.
Дата добавления: 2014-12-16; просмотров: 4014;
