Алгебраические уравнения

Одно уравнение с одним неизвестным

Рассмотрим одно алгебраическое уравнение с одним неизвестным х, вида:

f(x) = 0 (3),

например, sin(x) = 0.

Для решения таких уравнений MathCAD имеет встроенную функцию root( ), которая, в зависимости от типа задачи, может включать либо два, либо четыре аргумента.

- root(f(х),х);

- root(f(х),х,а,b);

Лекция 9 45

f(х) — скалярная функция, определяющая левую часть уравнения (3); х — скалярная переменная, относительно которой решается уравнение; а,b — границы интервала, внутри которого происходит поиск корня.

В первом случае необходимо задать начальное значение переменной х, просто предварительно присвоить х некоторое число. Корень уравнения ищется вблизи этого числа.

На Рис. 25 приведен пример решения уравнения sin(x) = 0,при начальном приближении х = 0,5.

x:= 0.5

f(x) := sin(x)

solution:= root(f(x) , x) solution= 0

Рис. 25. Поиск корня нелинейного алгебраического уравнения.

Хотя уравнение имеет бесконечное множество корней xn= n×π(n = 0, ±1, ±2,...), MathCAD находит только один из них, х = 0, наиболее близкий к начальному приближению х=0.5.

Если задать другое начальное значение, например х = 3, то решением будет другой корень уравнения х = πи так далее.

Таким образом, для поиска корня требуется его предварительная локализация. Это связано с особенностями численного метода решения уравнения - метода секущих.

Если уравнение неразрешимо, то будет выдано сообщение об ошибке.

Иногда удобнее задавать не начальное приближение к корню, а интервал [а,b], внутри которого корень заведомо находится. В этом случае следует использовать функцию root( ) с четырьмя аргументами (Рис. 26.). Начальное значение х присваивать не нужно, так как поиск корня осуществляется на интервале [а,b]. Функцию f(х) можно записать в теле функции root(

) в явном виде (Рис. 26.).

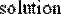
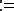
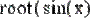
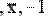
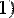
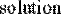
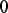
Рис. 26. Поиск корня алгебраического уравнения на заданном интервале.

Лекция 9 46

Когда root( ) имеет четыре аргумента, следует помнить о двух ее особенностях:

- внутри интервала [а,b] не должно находиться более одного корня, иначе будет найден один из них, заранее неизвестно, какой именно;

- значения f(а) и f(b) должны иметь разный знак, иначе будет выдано сообщение об ошибке.

Если уравнение не имеет действительных корней, но имеет мнимые, то их также можно найти.

Системы уравнений

Рассмотрим решение системы нелинейных уравнений. Для простоты предположим, что система состоит из N уравнений с N неизвестными:

f1(x1, ... ,хN) = 0,

. . . (4)

fN(x1, ... ,хN) = 0,

Здесь f1(x1, ... ,хN) , ..., fN(x1, ... ,хN) — некоторые скалярные функции от скалярных переменных

х1, х2, ... хN.

Для решения систем в MathCAD используется специальный вычислительный блок

Given/Find, состоящий из трех частей, идущих последовательно друг за другом:

- Given – ключевое слово;

- система, записанная логическими равенствами;

- Find(x1... ,хN) — встроенная функция для решения системы относительно переменных

х1, х2, ... хN.

Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения для всех х1, х2, ... хNдо ключевого слова Given.

Функция Find( ) возвращает вектор, составленный из корней системы (4). Таким образом, число аргументов функции Find( ) должно быть равно числу неизвестных.

На Рис. 27. приведен пример решения системы двух уравнений с двумя неизвестными.

Лекция 9 47

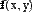
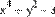
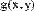
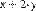
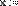
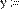
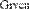
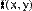
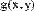
Рис. 27. Решение системы уравнений.

В первых двух строках вводятся функции, определяющие левые части уравнений системы.

Затем переменным х и у присваиваются начальные значения. После этого следует ключевое слово Given и два логических равенства, выражающих систему уравнений. Завершает вычислительный блок функция Find( ), значение которой присваивается вектору v.

Следующая строка показывает содержание вектора v, т. е. решение системы. Элемент вектора v0 есть первый аргумент функции Find( ), то есть неизвестное х, элемент v1–второй аргумент функции Find( ), то есть неизвестное у.

Уравнения системы можно записывать непосредственно внутри вычислительного блока, то есть не определять заранее функции f(x,y) и g(х,у), а сразу написать:

Given

4 2

x + y 3

x + 2 y 0

В вычислительный блок можно добавить дополнительные условия в виде неравенств. Например, ввод ограничения на поиск только отрицательных значений х приведет к нахождению другого корня (Рис. 28).

x:= 1

Given

y:= 1

x4+ y2 3

x+ 2y 0 x< 0

v:= find(x, y)

æ -1.269ö

Дополнительное неравенство

v= ç ÷

è 0.635ø

Рис. 28. Решение системы уравнений и неравенств.

Лекция 9 48

Несмотря на те же начальные значения, мы получили другой корень. Это произошло именно благодаря дополнительному неравенству в блоке Given/Find.

Если система не имеет решения (несовместна), MathCAD выдаст сообщение об ошибке, гласящее, что решения не найдено, и предложение попробовать поменять начальные значения.

Вычислительным блоком Given/Find можно найти и корень одного уравнения с одним неизвестным.

В этом случае система считается состоящей из одного уравнения. Единственным отличием будет то, что функция Find( ) возвращает скаляр, а не вектор (Рис. 29.).

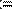
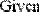
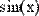
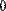
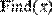
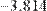
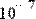
Рис. 29. Поиск корня уравнения с одним неизвестным с помощью блока Given/Find.

Лекция 9 49