Численные вычисления

Численное интегрирование

Численное интегрирование в MathCAD реализовано в виде оператора определенного интеграла, позволяющего вычислять интегралы от скалярных функций в скалярных пределах интегрирования.

Операторы численного интегрирования

Чтобы вычислить определенный интеграл, следует напечатать его оператор с помощью панели Calculus (Вычисления) (Рис. 1) нажатием кнопки со значком определенного интеграла, или сочетанием клавиш <Shift>+<7> (&).

Появится символ интеграла с несколькими местозаполнителями (Рис. 1), в которые нужно ввести нижний и верхний пределы интегрирования, подынтегральную функцию и переменную интегрирования.

Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела нужно ввести символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести минус бесконечность, нужно добавить знак минус к символу бесконечности, как к обычному числу.

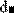
Рис. 1. Оператор интегрирования.

Чтобы получить результат интегрирования, следует ввести знак равенства (Рис. 2).

Лекция 9 50

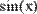
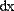
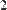
Рис. 2. Численное вычисление определенного интеграла.

Подынтегральная функция может зависеть от любого количества переменных. Для того чтобы указать, по какой переменной вычисляется интеграл, нужно ввести ее имя в соответствующий местозаполнитель. Для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция (Рис. 3).

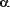
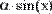
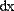
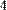
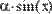
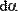
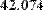
Рис. 3. Интегрирование функции двух переменных по разным переменным.

Оператор интегрирования может использоваться для вычисления функций от ранжированных переменных.

Пример присваивания пользовательской функции g(α) значения определенного интеграла и вычисления нескольких ее значений приведен на Рис. 4.

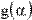
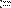
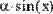
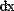
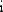
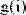
Рис. 4. Использование оператора интегрирования в функции пользователя.

Лекция 9 51

Численное дифференцирование

В MathCAD можно вычислять производные скалярных функций любого количества аргументов, от 0-го до 5-го порядка включительно. И функции, и аргументы могут быть как действительными, так и комплексными. Невозможно дифференцирование функций только вблизи точек их сингулярности.

Первая производная

Для того чтобы продифференцировать функцию f(х) в некоторой точке:

- нужно определить точку х, в которой будет вычислена производная, например х:=1;

- ввести оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или ввести с клавиатуры вопросительный знак <?>;

- В появившихся местозаполнителях (Рис. 5) ввести функцию f(х), и имя самого аргумента х;

- нажать клавишу "равно" для получения ответа.

Рис. 5. Оператор дифференцирования.

Пример дифференцирования функции f(x)=cos(x)ln(x) приведен на Рис. 6.

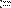
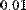
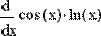
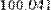
Рис. 6. Численное дифференцирование.

Если функция вводится явно в оператор дифференцирования, то необходимо предварительно определять точку, в которой производится численное дифференцирование, как это сделано в первой строке Рис. 6. Иначе будет выдано сообщение об ошибке, гласящее, что переменная или функция, входящая в выражение, ранее не определена.

Можно предварительно определить функцию в отдельном выражении, а затем посчитать ее производную в заданной точке (Рис. 7.).

Лекция 9 52

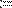
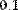
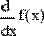
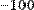
Рис. 7. Символьное и численное дифференцирование функции пользователя.

Можно также применить оператор дифференцирования для определения собственных функций пользователя (Рис. 8).

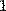
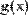
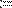
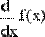
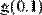
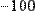
Рис. 8. Определение функции пользователя через оператор дифференцирования.

В обоих рисунках первой строкой определяется функция f(x)=1/x. Во второй строке Рис.7 численно определяются значения этой производной в точке х=0.1. На Рис. 8 через производную от f(х) определяется еще одна пользовательская функция g(х) и затем находится ее конкретное значение в той же точке х=0.1.

Для численного дифференцирования MathCAD вычисляет производную с колоссальной точностью до 7-8-го знака после запятой.

Производные высших порядков

MathCAD позволяет численно определять производные высших порядков, до 5-го включительно. Чтобы вычислить производную N-го порядка функции f(х) в точке х, нужно проделать те же самые действия, что и при взятии первой производной, но вместо оператора производной необходимо применить оператор N-й производной (Nth Derivative) с той же панели Calculus (Вычисления) либо с клавиатуры нажатием клавиш <Ctrl>+<?>. Этот

оператор содержит еще два местозаполнителя, в которые следует поместить число N – порядок производной, причем определение порядка производной в одном из местозаполнителей приводит к автоматическому появлению того же числа в другом из них.

Рис. 9 демонстрирует численное вычисление второй производной. Как и при вычислении обычной производной, необходимо перед оператором дифференцирования присвоить аргументу функции значение, для которого будет вычисляться производная.

Лекция 9 53

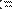
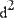
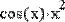
Рис. 9. Численное вычисление второй производной.

Чтобы вычислить производную порядка выше 5-го, следует последовательно применить несколько раз оператор N-й производной. На Рис. 10 численно вычисляется производная седьмого порядка синуса в точке х=0.1.

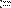
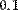
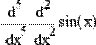
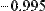
Рис. 10. Численное вычисление седьмой производной.