Системы линейных алгебраических уравнений

Множество, если не сказать большинство, задач вычислительной математики сводится к решению систем линейных алгебраических уравнений (СЛАУ), т. е. систем уравнений вида:

аi1х1+аi2х2+. . .+ainхn= bi, где i = 1, 2, …, n (1)

В матричной форме СЛАУ записывается в виде:

А×х = В (2)

где А – матрица коэффициентов СЛАУ размерности n х n,

х — вектор неизвестных, В – вектор правых частей уравнений.

СЛАУ имеет единственное решение, если матрица коэффициентов А является невырожденной, (несингулярной), то есть если ее определитель не равен нулю.

В MathCAD СЛАУ можно решить тремя способами:

- с помощью обратной матрицы (Рис. 15);

- с помощью встроенной функции lsolve( ) (название lsolve происходит от line solving) (Рис. 16);

- с помощью вычислительного блока Given/Find (Рис. 17).

Например, нужно решить систему линейных алгебраических уравнений вида:

.

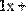
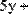
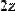
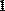
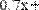
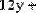
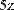
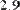
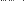
Система состоит из трех уравнений с тремя неизвестными. Проиллюстрируем решение системы перечисленными тремя методами.

Метод обратной матрицы

Задаем матрицу коэффициентов А и вектор правых частей В.

Лекция 9 40

æç 1

5 2÷ö

æç 1÷ö

A:=ç 0.7 12 5÷

b:=ç 2.9÷

ç 3 0 4÷

ç 3.1÷

è ø è ø

Записываем формулу вычисления корней, через обратную матрицу и выводим результаты:

æç xö÷

-

ç y÷ := A 1×b

ç z÷

è ø

x= -0.186

y= -0.129

z= 0.915

Рис. 15. Решение СЛАУ методом обратной матрицы.

Метод встроенной функции lsolve( ).

Задаем матрицу коэффициентов А и вектор правых частей В, если они еще не заданы и выводим результат, используя вычислительную функцию lsolve( ):

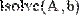
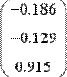
Рис. 16. Решение СЛАУ с помощью встроенной функции lsolve( ).

Метод решающего блока Given/Find.

Задаем начальные приближения для неизвестных

(любые числа)

Вводим ключевое слово Given

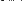
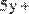Переписываем систему уравнений в виде логических равенств, используя знак сравнения

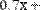
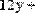
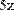
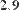
(Булево равенство) , который вводится

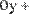комбинацией клавиш <Ctrl> + < = > или кнопкой на панели

Лекция 9 41

Выводим результат, используя функцию Find( ),

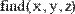причем число аргументов функции Find( ) должно быть равно числу неизвестных.

Рис. 17. Решение СЛАУ использованием вычислительного блока Given/Find.

Задание начальных условий необходимо, так как решающий блок Given/Find

использует итерационные методы вычислений.

Корни СЛАУ, полученные всеми тремя методами должны совпадать.

Встроенные операторы суммирования и произведения.

Оператор	Клавиши	Описание
å =	<Ctrl>+<Shift>+<4>	Сумма
å	<Shift>+<4>	Сумма ранжированной переменной
Õ =	<Ctrl>+<Shift>+<3>	Произведение
Õ	<Shift>+<3>	Произведение ранжированной переменной

Эти операторы вводятся нажатием соответствующих кнопок на панели Calculus

(Вычисления) , которая вызывается с панели Math (Математика) .

Лекция 9 42

Функция условия if( )

Функция условия позволяет задавать варианты вычислений в зависимости от выполнения условия. Она имеет вид: if(cond, x,y), где cond – логическое условие, х, – значение, возвращаемое, если условие истинно, у – значение, возвращаемое, если условие ложно (Рис. 18.).

t:= 0, 0.02p .. 2p

f(t) := if(t£ p , sin(t) , -sin(t))

1

f(t)

0

1 0 5 10

T

Рис. 18. Функция условия.

На Рис. 18 показан способ, при котором функция условия вводится с клавиатуры. Возможен другой способ задания условной функции при помощи панели инструментов

Programming (Программирование) (Рис. 19), которая вызывается с панели Math (Математика).

Рис. 19. Панель инструментов Programming (Программирование)

Чтобы задать условную функцию, на панели инструментов Programming (Программирование) нужно нажать кнопку Add Line (Добавить строку программы), после чего вставляется вертикальная черта с двумя местозаполнителями.

В верхний местозаполнитель нажатием кнопки if вставляется функция условия if, а в нижний местозаполнитель нажатием соответствующей кнопки вводится ключевое слово otherwise, (которое переводится: «в остальных случаях»). В появившиеся местозаполнители вводятся условные и вычислительные выражения (Рис. 20), так что верхняя строка имитирует выполнение условия, а нижняя строка имитирует альтернативный вариант.

Лекция 9 43

f(t) :=

f(t) :=